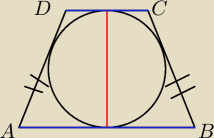
@@@ qu: Udowodnij że średnica okręgu wpisanego w trapez równoramienny, ma długość równą średniej geometrycznej długości podstaw trapezu.

wredulus_pospolitus:

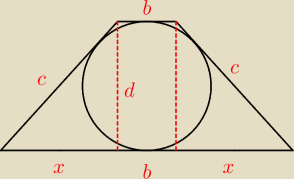
	a−b
x =
	2

	a+b
c =		<−−− patrz suma przeciwległych boków czworokąta opisanego na okręgu jest sobie
	2

równa czyli: x² + d² = c²

(a−b)2		(a+b)2
	+ d2 =
4		4

4d² = 4a*b d² = a*b d = √a*b c.n.w.

qu: drugie zadanie które dziś zrozumiałem , dziękuję

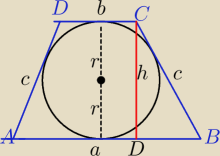Mila: Z.Trapez ABCD− trapez równoramienny opsany na okręgu T.2r=√a*b h=2r −średnica okręgu

	a+b
a+b=2c własność dla czworokąta opisanego na okręgu⇔c=
	2

	a−b
|DB|=
	2

w Δ CDB: c²=h²+|DB|²

	a+b		a−b
h2=(		)2−(		)2
	2		2

	a2+2ab+b2		a2−2ab+b2
h2=		−		⇔
	4		4

	a2+2ab+b2−a2+2ab−b2
h2=
	4

h²=a*b h=√a*b cnw

wredulus_pospolitus: Miluś ... toć ja dokładnie to samo napisałem

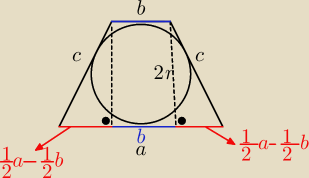agulka: Należy udowodnić, że 2r=√ab⇒4r²=ab Skorzystaj z twierdzenia, że jeżeli czworokąt można opisać na okręgu, to sumy jego

	a+b		1		1		1
przeciwległych boków są równe, czyli a+b=2c⇒c=		⇒c2=		a2+		ab+		b2
	2		4		2		4

	1		1
c2=(2r)2+ (		a−		b)2
	2		2

	1		1
c2=4r2+(		a−		b)2
	2		2

1		1		1		1		1		1
	a2+		ab+		b2−		a2+		ab−		b2=4r2
4		2		4		4		2		4

4r²=ab

Mila: Arturku, długo pisałam i nie widziałam Twojego wpisu.

qu: Dzięki wszystkim

wredulus_pospolitus: heh ... widzę że dzisiaj Panie piękne rysunki dziergają na laptopach

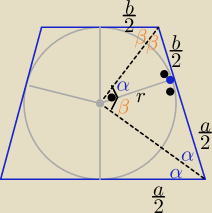Eta: z podobieństwa trójkątów :

b   2		r		ab		1
	=		⇒ r2=		⇒ r=		√ab to 2r= √ab
r		a   2		4		2

qu: skąd wiesz, że na laptopach?

Mila: Artur wszystko wie, nie tylko z matematyki. Dobranoc.

Eta: No przecież ,że nie "na drutach" ?

qu: A już myślałem ...... Koniec już na dziś ?

bezendu: Eta zajrzysz do mojego tematu ?