Rozwiąż Bartek: Hey , mam pytanie , pytałem o podobne zadanie ale tutaj nie wiem jak dalej ruszyć: (²₃)^x2−3 >= ⁹₄ najbardziej mi w tym zadaniu ten x² przeszkadza

J:

	2
P = (		)−2 i funkcja jest malejąca.
	3

J:

	2		2
(		)x2 − 3 ≥ (		)−2 ⇔ x2 − 3 ≤ −2
	3		3

Bartek: to mogę tak opuścić te podstawy , bo wcześniej uzyskałem odpowiedź ,ze jak są jakieś działania to nie mogę tak robić : 'opuścić' podstawy możesz dopiero jeżeli masz: a^b = a^c

J:

	2
No a tu masz tą samą podstawę :
	3

Bartek: https://matematykaszkolna.pl/forum/237203.html tu miałem podobne zadanie i nie mogłem tak robić , chyba sie pogubiłem

Bartek: Aaaa , chyba zrozumiałem , w tym po jednej i drugiej stronie jest tylko jedna podstawa i można tak zrobić ale jesli po jedenej stronie jest więcej działań , wtedy nie można tak ?

J: Jesli masz równanie: a^b = a^c ⇔ b =c Jesli masz nierówność: a^b > a^c ⇔ b > c , gdy a > 1 ( bo funkcja jest rosnąca ) Jesli masz nierówność: a^b > a^c ⇔ b < c , gdy a ∊ (0,1) ( bo funkcja jest malejąca )

J: Tak.Musi być jedna i taka sama podstawa.

Janek191:

	2		9
(		)x2 − 3 ≥
	3		4

	2		3
(		)x2 − 3 ≥ (		)2
	3		2

	2		2
(		)x2 − 3 ≥ (		)−2
	3		3

zatem

	2
x2 − 3 ≤ − 2 , bo podstawa		< 1
	3

x² ≤ 1 x ∊ < − 1; 1 > ==========

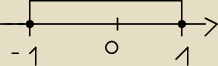
Bartek: to będzie do tego rozwiązaniem ?

J: