 Półprosta poprowadzona z wierzchołka kąta prostego trójkąta prostokątnego
i przechodząca przez
środek okręgu wpisanego w trójkąt dzieli przeciwprostokątną w stosunku 3:4. Oblicz pole
trójkąta,
jeśli przeciwprostokątna ma długość 20.
Półprosta poprowadzona z wierzchołka kąta prostego trójkąta prostokątnego
i przechodząca przez
środek okręgu wpisanego w trójkąt dzieli przeciwprostokątną w stosunku 3:4. Oblicz pole
trójkąta,
jeśli przeciwprostokątna ma długość 20.
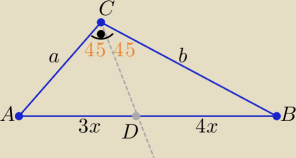 Półprosta, która przechodzi przez środek okręgu wpisanego w ten trójkąt
jest dwusieczną kąta prostego
to z twierdzenia o dwusiecznej:
Półprosta, która przechodzi przez środek okręgu wpisanego w ten trójkąt
jest dwusieczną kąta prostego
to z twierdzenia o dwusiecznej:
| a | b | 3 | |||
= | , x>0 ⇒ a= | b i |AB|= 20 | |||
| 3x | 4x | 4 |
| 9 | ||
z tw. Pitagorasa | b2+b2=400⇒ b=........ i a=...... | |
| 16 |
| a*b | ||
P= | =......... | |
| 2 |

 Jeszcze nie do końca wiem jak rozwiązać te zadanie
W trapezie (dowolnym) ABCD punkt O jest punktem przecięcia przekątnych oraz AB||CD. Oblicz
pole trapezu, jeŜeli pole trójkąta ABO wynosi 25, a pole trójkąta CDO wynosi 9
Jeszcze nie do końca wiem jak rozwiązać te zadanie
W trapezie (dowolnym) ABCD punkt O jest punktem przecięcia przekątnych oraz AB||CD. Oblicz
pole trapezu, jeŜeli pole trójkąta ABO wynosi 25, a pole trójkąta CDO wynosi 9


