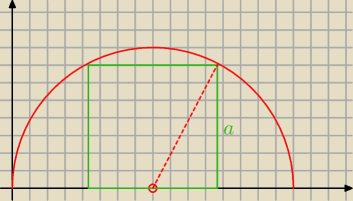
 W półkole o promieniu długości 8 wpisano kwadrat w ten sposób, że jeden z
boków kwadratu
zawiera
się w średnicy, a dwa wierzchołki należą do półokręgu. Oblicz stosunek pola kwadratu do pola
półkola.
Zad.2
Półprosta poprowadzona z wierzchołka kąta prostego trójkąta prostokątnego i przechodząca przez
środek okręgu wpisanego w trójkąt dzieli przeciwprostokątną w stosunku 3:4. Oblicz pole
trójkąta,
jeśli przeciwprostokątna ma długość 20.
W półkole o promieniu długości 8 wpisano kwadrat w ten sposób, że jeden z
boków kwadratu
zawiera
się w średnicy, a dwa wierzchołki należą do półokręgu. Oblicz stosunek pola kwadratu do pola
półkola.
Zad.2
Półprosta poprowadzona z wierzchołka kąta prostego trójkąta prostokątnego i przechodząca przez
środek okręgu wpisanego w trójkąt dzieli przeciwprostokątną w stosunku 3:4. Oblicz pole
trójkąta,
jeśli przeciwprostokątna ma długość 20.

 1.
1.
| a2 | ||
a2+ | =64 5a2=256 a2=... | |
| 4 |
| a2 | 4 | |||
a2+ | =R2 ⇒ a2= | R2= 0,8R2= P(kwadratu} , P(półkola)=0,5πR2 | ||
| 4 | 5 |
| 0,8R2 | 8 | |||
k= | = | |||
| 0,5πR2 | 5π |
 − z tw. o dwusiecznej
− 5k=20 ⇒ k=4
− P=6k2= 96
− z tw. o dwusiecznej
− 5k=20 ⇒ k=4
− P=6k2= 96
 .
.
 Miłych snów
Miłych snów 
 .
.



 !
!