Napisz równania tych stycznych Zosia: Napisz równania tych stycznych do wykresu funkcji f(x) =x³ − 8x,

	1
które są prostopadle do prostej y =		x + 3.
	2

Jak rozwiązać bez użycia pochodnej? mamy równą y = −2x + b₁ jednak nie mogę ułożyć ukł. rów.

Bizon: ... a dlaczego bez pochodnych ?

Zosia: Ponieważ nie umiem zastosować pochodnej, przyg. się do matury nie chcę mieszać sobie niepotrzebnie w głowie. lub Jeśli obliczenie pochodnej nie jest na tyle skomplikowane i możesz mi pokazać jak policzyć dla danego przypadku.

Zosia: czy mogę prosić o wskazówki, pomoc?

Bizon: pochodna tej funkcji jest prościutka do policzenia f'(x)=3x²−8

Bizon: musimy na wykresie funkcji znaleźć punkty w których styczna do funkcji jest

	1
jednocześnie prostopadła do y=		+3
	2

Zatem 3x²−8=−2 ⇒ 3x²=6 x²=2 x₁=−√2 x₂=√2 Teraz ze wzoru funkcji ustalisz y₁ i y₂ i napiszesz równania

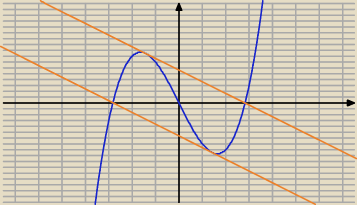
Bogdan: y = x³ − 8x, styczne: y = −2x − 4√2 oraz y = −2x + 4√32 Jak bez pochodnej, to bez niej. Można te styczne wyznaczyć w ten sposób: Styczna y = −2x + b Styczna ma z krzywą punkt wspólny, czyli w tym przypadku x³ − 8x = −2x + b

	b
x3 − 8x + 2x − b = 0 ⇒ x(x2 − 8) + 2(x −		) = 0
	2

	b
x(x − √8)(x + √8) + 2(x −		) = 0
	2

b		√8
	= √8 lub		= −√8 ⇒ b = √32 = 4√2 lub b = −√32 = −4√2
2		2

Bizon: ... "naciągane" to aż trzeszczy − Z przyrównania prostej do krzywej ... nie wynika NIC

Bogdan: a masz inną propozycję bez zastosowania pochodnej?

Bizon: gdybym miał to podałbym ...ale nie pisałbym herezji ...

Bogdan: Pokaż, gdzie widzisz tę herezję?, a może nie zrozumiałeś rozwiązania, które zaproponowałem?

Bizon:

	b
a jakich to reguł matematycznych użyłeś aby z x(x−√8)(x+√8)+2(x−		)=0
	2

"wyliczyć" te dwie wartości b

Bizon: ... chyba nie tylko ja nie zrozumiałem rozwiązania które zaproponowałeś ...

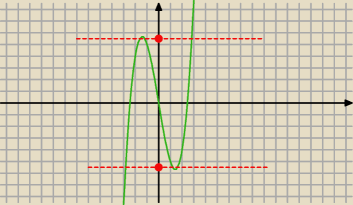
Bizon: należałoby wyszukać dla x³−8x+2x=b takie b aby miały dwa punkty wspólne (nie 1 i nie 3) x³−6x=b ... i to są te b

Zosia: zwątpiłam, że ktokolwiek odpisze tak tylko x(x² − 6)= b x=0 lub x=√6 znalazłam rozw. b₁= −4√2 b₂=4√2 czy mogę prosić o skomentowanie tematu z :https://matematykaszkolna.pl/forum/235818.html czekam i czekam, ale nie odp. brak jakiejkolwiek

Zosia: dwa punkty wspólne funkcji x³ − 6x = b oraz x³ − 8x= 0

Bizon: ... to zupełnie nie o t chodzi Zosiu ... trzeba znaleźć takie b aby x³−6x=b miało 2 rozwiązania ... pokazałem to graficznie Z tego otrzymamy b=−4√2 lub b=4√2 (to co Bogdan "naciągnął") Takie b należałoby wstawić do równania y=−2x+b

Zosia: ok, rozumiem kolejne pytanie jak szukać? x³ − 6x = b ?

Bizon: chyba tylko graficznie ... Inna metoda to znów pochodne −

Zosia: graficznie więc muszę zgadywać, nie mogę tego obliczyć.

Bizon: ... można obliczyć ...ale znów z pochodną ... ale skoro z pochodną to po co "przez Poznań" − Sposób z pochodną pokazaliśmy ma początku. −

Bizon: ...a tamto zadanko odnalazłaś ? − https://matematykaszkolna.pl/forum/235818.html