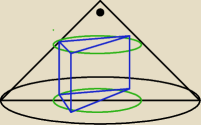
 Dany jest stozek o promieniu podstawy 15, ktorego przekroj osiowy jest trojkatem prostokatnym.
W stozek ten wpisano graniastoslup prosty majacy w podstawie trojkat prostokatny, w ktorym
stosunek przyprostokatnych jest rowny 3:4. Jedna podstawa graniastosupa zawiera sie w
podstawie stozka, a wierzcholki drugiej podstawy naleza do pobocznicy stozka. Zbadaj, jakie
powiny byc dl. krawedzi podstawy i wys graniastosupa, aby pole jego pow bylo najwieksze.
Czy przekrój jest poprawny? Jeśli mogę prosić o rysunek
Rozw:
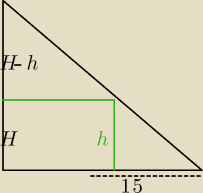
H− wys. stożka
h− wys. ostrosłupa
3a , 4a −przyprost. podstawy ostrosłupa
5a − przeciwprost. ostrosłupa
Dany jest stozek o promieniu podstawy 15, ktorego przekroj osiowy jest trojkatem prostokatnym.
W stozek ten wpisano graniastoslup prosty majacy w podstawie trojkat prostokatny, w ktorym
stosunek przyprostokatnych jest rowny 3:4. Jedna podstawa graniastosupa zawiera sie w
podstawie stozka, a wierzcholki drugiej podstawy naleza do pobocznicy stozka. Zbadaj, jakie
powiny byc dl. krawedzi podstawy i wys graniastosupa, aby pole jego pow bylo najwieksze.
Czy przekrój jest poprawny? Jeśli mogę prosić o rysunek
Rozw:
H− wys. stożka
h− wys. ostrosłupa
3a , 4a −przyprost. podstawy ostrosłupa
5a − przeciwprost. ostrosłupa
| H | 15 | ||
= | |||
| H −h | 2,5a |
| h(6−a) | ||
h= | ||
| 6 |






| H | 15 | |||
dotąd było ok | = | 15*2,5a=225−15h | ||
| H−h | 2,5a |
| 225−37,5a | ||
h= | ⇒ h=15−2,5a | |
| 15 |
| 3a*4a | ||
Pol podstawy graniastosłupa to | =6a2 | |
| 2 |