Marcin: W trójkącie mamy dane: |AC| = √3 i |∡ACB| = 90°. Przez wierzchołek C poprowadzono prostą, która utworzyła z bokiem AC kąt 60° i przecięła bok AB w punkcie D tak, że |AD| : |DB| = 1:3 Oblicz długość boków AB i BC oraz długość odcinka CD. Powiedzcie mi czy stworzyłem do tego dobre równanie i czy mogę z niego policzyć moje niewiadome. 2xtw cosinusów. i pitagoras:

⎧	x2=y2+3−√3y
⎨	9x2=z2+y2−√3x
⎩	3+z2=16x2

bezendu: Widzę arkusze Pazdro lecą ?

Marcin: A nie wiem, dostałem od nauczycielki i mam podpisane: "próbny arkusz maturalny R−1" Cześć bezendu, jak tam ferie i nauka?

bezendu: A bardzo dobrze, od rana do wieczora robię zadania, muszę nadrobić zaległości, żeby się w maju nie ośmieszyć wynikiem. Dobrze masz te równania.

Marcin: Tam zaraz ośmieszyć Dzięki

bezendu:

Marcin: Druga sprawa to obliczenie tego. Jest dość dużo rachunków

bezendu: Nie masz odpowiedzi ?

Marcin: Nie mam. Dostałem same zadania

bezendu: Nie chcę za Ciebie rozwiązywać.

Saizou : cześć chłopaki Marcin pomyśl nad tw. sinusów

Saizou : a jak chcesz to mogę to rozwiązać

Marcin: Zauważyłem że mogę skorzystać z twierdzenia sinusów jak już miałem ten układ i ambitnie do tego podszedłem, dlatego próbuje to ciągle rozwiązać Napisz swoje rozwiązania, porównam sobie wynik

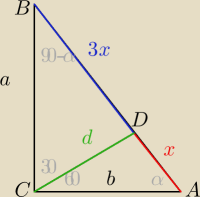
Saizou : b=√3 z tw. sinusów otrzymamy

d		x
	=
sinα		sin60

d		3x
	=
sin(90−α)		sin30

d		2√3		2√3
	=		x →d=		x*sinα
sinα		3		3

d
	=6x →d=6x*cosα
cosα

2√3
	x*sinα=6x*cosα
3

2√3sinα=18cosα

cosα		2√3		√3
	=		=		=ctgα
sinα		18		9

	√3
ctgα=
	a

√3		√3
	=		→a=9
a		9

9²+√3²=(4x)² 81+3=16x²

84
	=x2
16

21
	=x2
4

	√21
x=
	2

4x=2√21 i z tw. cosinusów x²=b²+d²−2bdcos60

21
	=3+d2−√3d
4

21=12+4d²−4√3d 4d²−4√3d−9=0

	3√3
d=
	2

za wyniki nie odpowiadam

Marcin: Szybki jesteś

Saizou : bo miałem wcześniej to napisane, tylko nie chciałem wrzucać

bezendu: Marcin ile Ty tego pijesz ? Jutro do szkoły idziesz...

Marcin: Domyśliłem się, ale chciałem CI komplement sprawić Biorę się za kolejne zadanie

Marcin: bezendu Od teraz tylko soczek

Saizou : Marcinie matematyką trzeba się rozkoszować a nie liczyć na łeb na szyje

Marcin: No rozkoszuję się!

Marcin:

	4
Wytłumaczcie mi skąd w rozwiązaniu dudusia wzięło się po tym dzieleniu		. Dlaczego nie
	x+2

samo 4? https://matematykaszkolna.pl/forum/22021.html

Eta: Skąd ja znam "dudusia"?

bezendu: Czyżby Eta ?

Saizou : może to lepiej pokaże to co tam było zrobione

x4−4x2+x+6		x4+2x3−2x3−4x2+x+2+4
	=		=
x+2		x+2

	x3(x+2)−2x2(x+2)+1(x+2)+4
=		=
	x+2

x3(x+2)		2x2(x+2)		1(x+2)		4
	−		+		+		=
x+2		x+2		x+2		x+2

	4
x3−2x2+1+
	x+2

bezendu: A ja wolę podzielić tak jak duduś Marcin czy następne zadania jest z rękawiczkami ?

Eta:

	4
9:5= 1+
	5

Marcin: Bezendu następne to obliczenie wartosci wyrażenia z logarytmami A nie można tego schematem Hornera zrobić? Mi wyszły wszystkie współczynniki takie same, a reszta równa 4. ( u dudusia reszta też jest równa 4)

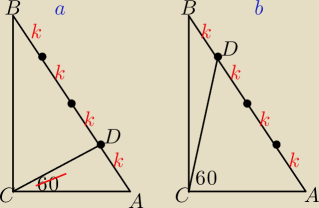
Bogdan: Dane w zadaniu: |AC| = √3 i |∡ACB| = 90°. Przez wierzchołek C poprowadzono prostą, która utworzyła z bokiem AC kąt 60° i przecięła bok AB w punkcie D tak, że |AD| : |DB| = 1:3 Na rysunku a |AD| : |DB| = 1 : 3, ale miara kąta ACD nie może być równa 60^o. Na rysunku b miara kąta ACD może być równa 60^o, ale |AD| : |DB| nie może być równe 1 : 3 I co w tej sprawie Marcinie powiesz?

Marcin: Na swoim rysunku też mi 60st tam nie pasowało. Według mnie ten kąt przy AC powinien mieć 30st, ale taką mam treść zadania w arkuszu i nic nie poradzę.

Bogdan: Po prostu dane w tym zadaniu są sprzeczne. Saizou wykonał obliczenia na podstawie błędnie sporządzonego rysunku, odcinek 3x dłuższy od odcinka x, a to oznacza, że naprzeciw boku 3x jest kąt o większej mierze od kąta leżącego naprzeciw boku o długości x (u Saizou jest odwrotnie).

Marcin: To jest zadanie z arkuszy maturalnych i takie tam są dane Co mam w takim razie napisać nauczycielce w odpowiedzi? Dane są sprzeczne?

Saizou : tak jak na maturze próbnej z OKE ze stycznia zadanie na optymalizacje z trójkątem. Istnieje tylko jeden taki trójkąt