Matura. Marcin: Poprosiłbym o jakieś zadanie i późniejsze podpowiedzi, albo sprawdzenie moich obliczeń

zawodus: Zadanie czego ma dotyczyć?

ICSP: Czy istnieje liczba naturalna n, dla której liczba n⁴ + 4n³ + 7n² + 3 jest kwadratem liczby całkowitej ?

zawodus: Nie zbyt ambitne jak na maturę?

Marcin: Ogólnie chodzi o maturę, także dotyczyć może wszystkiego co może się na niej znaleźć

ICSP: Na pewno prostsze od twojego wielomianu

zawodus: Moje nie było na maturę tylko znalazłem je w podręczniki do lo i się zastanawiałem po co tam się znalazło

zawodus: dobra Marcin czekamy na rozwiązanie...

Marcin: Nie bardzo wiem jak się za to zabrać. Mam rozbijać ten wielomian?

Marcin: Ewentualnie mogę sprawdzać na piechotę. Na maturze dostałbym za to punkty, serio

maturzysta14: też porposze o jakieś zadania zarówno jesli chodzi o zakres podstawowy jak i rozszerzony

Marcin: maturzysta14, a to moje zadanie jesteś w stanie rozwiązać?

Saizou : Marcin jeśli byś pokazał że coś takiego jest to ok, bo masz za zadanie wykazać czy istnieje takie n dla którego wielomian jest kwadratem liczby całkowitej

Bogdan: Powtarzam Marcinie zadanie, które Ci zaproponowałem. 1) Wyznaczyć zależność między miarą kąta nachylenia ściany bocznej dowolnego ostrosłupa prawidłowego do płaszczyzny podstawy i miarą kąta β nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa. I kolejne zadanie. 2)Mamy 5 wielościanów foremnych: czworościan, sześcian, ośmiościan, dwunastościan i dwudziestościan. Dlaczego nie istnieje więcej wielościanów foremnych? Odpowiedź uzasadnić.

Mila: 1) Wyznacz wszystkie wartości parametru m, dla ktorych równanie: 2x²+(3−2m)x−m+1=0 ma dwa różne rozwiazania x₁, x₂ takie , że: |x₁−x₂|=3 2) Oblicz najmniejszą wartość wielomianu: (x−1)*(x−2)*(x−3)*(x−4)+4

maturzysta14: Marcin, staram się ale narazie brak skutecznych pomysłów.

Marcin: Panie Bogdanie to 1 zadanie próbowałem, próbowałem, ale po wyliczeniu tego dla różnych ostrosłupów prawidłowych nie mam koncepcji co do dalszego rozwiązania

alojzy: Bogdan twoje zadania są zdecydowanie nie związane z maturą..

alojzy: Mila zadanie 2 bardzo ciekawe, pierwsze w miarę standard.

maturzysta14: Mila 1. −5/2 i 7/2 ?

alojzy: Mila zadanie drugie to 3 tak?

5-latek: Nie bede Cie meczyl trudnym zadaniem . Graniastoslop prawidlowy trojkatny ktorego wszystkie krawedzue maja dlugosc a rozcieto na dwa wielosciany plaszczyzna przechodzaca przez krawedz podstawy i nachylona to podstawy pod katem alfa Obliczyc stosunek objetosci wieloscianu zawierajaca te podstawe do do objetosci drugiego wieloscianu Zadanie nr 2

	1
Rozwiaz rownanie sinx+cosx+tgx+ctgx=
	sinxcosx

Radek: 1) Od Pani Mili 2x²+(3−2m)x−m+1=0 Δ>0 (3−2m)²−8(−m+1)>0 9−12m+4m²+8m−8>0 4m²−4m+1>0 (2m−1)²>0

	1
m∊R/{		}
	2

|x₁−x₂|=3 p(x₁−x₂)²}=3 /² (x₁−x₂)²=9 x₁²−2x₁x₂+x₂²=9 (x₁+x₂)²−4x₁x₂=9

	2m−3		−m+1
(		)2−4		=9
	2		2

4m2−12m+9		−m+1
	−4*		=9 /4
4		2

dobrze myślę ?

Marcin: 1) od Pani Mili. Δ>0 (3−2m)²−4*2*(−m+1) 4m²−4m+1>0 Δ=0

	1
x∊ R/{		}
	2

(x₁−x₂)²=9 x₁² −2x₁x₂+x₂²=9 x₁² +2x₁x₂+x₂²−4x₁x₂=9 (x₁+x₂)²−4x₁x₂=9 I jedziemy dalej z Vietta

	−b		c
(		)2−4		=9
	2a		a

	−3+2m		−m+1
(		)2−4		=9
	2		2

Z tego wychodzi równanie kwadratowe i m₁=.. i m₂ =.. I to są nasze dwa m z treści zadania.

zawodus: 5−latex ctg już nie ma na maturze.

maturzysta14: mam tak jak wy x) w 2. zatrzymałem się na x⁴−10x³+35x²−50x+28 , jedyny pomysł to potraktować to pochodną (?)

Marcin: pochodną?

maturzysta14: tak, pochodną, jestem w liceum na profilu matematycznym i dodatkowo robilismy ten dział, całki mieliśmy przez ferie

zawodus: maturzysta14 pochodnych nie ma na maturze (obecnej) musisz wpaść na inny trick

zawodus: oczywiście sposób z pochodną jest ok, ale 80 maturzystów tego nie umie

maturzysta14: czyli gdybym zrobił to zadanie pochodną nie dostane punktów?!

zawodus: 80 % lub nawet około 90 %

Marcin: 90? więcej

zawodus: dostaniesz maksa, ale poszukaj innej metody niż pochodna

Piotr 10: Ja też jestem na profili mat − fiz, ale pochodnych to nie mieliśmy, a szkoda

zawodus: Słyszałem raz sytuację: Pani doktor pyta studentów: − mieliście w szkole pochodne i granice? − nie − to bardzo dobrze. Od razu was nauczę tak jak powinno być...

5-latek: zawodus no to trudno jak nie ma ctg A na studiach tez nie ? Pytam z ciekawosci

5-latek: Bo byc moze za dwa lata sie wybiore

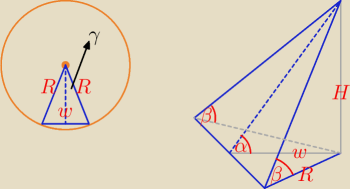
Bogdan: Podaję więc rozwiązanie zadania 1). Myślę − odpowiadając alojzemu − że maturzysta powinien umieć rozwiązać to zadanie. Narysowana bryła to fragment ostrosłupa prawidłowego. n − liczba wierzchołków (boków) wielokąta foremnego będącego podstawą ostrosłupa foremnego

	360o		180o
γ =		=
	2n		n

	180o
w = R cosγ = R*cos		(rysunek z okręgiem)
	n

H = w*tgα i H = R*tgβ ⇒ R cosγ*tgα = R tgβ

	180o		tgβ		180o
cos		=		albo cos		= tgβ ctgα
	n		tgα		n

Marcin: 5−latek w Twoim pierwszym zadaniu wysokość tego wielościanu zawierającego tą podstawę będzie

	a√3tgα
równa a−		? Czy kompletnie źle to liczę?
	2

zawodus: Na studiach nie wymyślają takich głupot o ile wiem i jest

zawodus: Bogdan ty uczysz w jakiejś elitarnej szkole? Przeciętny maturzysta nie ma pojęcia o co chodzi

Piotr 10: Mogę przedstawić swoje rozwiązanie do tego wielomianu ?

Marcin: Pewnie Piotr. Każdy się uczy, a zadań jest kilka

maturzysta14: wymnożyłem (x−1)(x−4)(x−2)(x−3)+4 = (x²−5x +4)(x²−5x+6)+4 t= x² − 5x+5 (t+1)(t−1)+4 iść w tą strone?

zawodus: maturzysta14 spróbuj i zobaczysz

maturzysta14: chyba nie poprosze o jakąś podpowiedź

Radek: Tak, podstawienie trzeb zrobić.

5-latek:

	a√3tgα
h=
	2

zawodus: maturzysta14 jak się będziesz poddawał to nigdy samemu żadnego zadania nie zrobisz...

maturzysta14: czyli wyjdzie 3 jako najmniejsza wartość 8)

Mila: Może tak : Założenia jak u Radka i Marcina, .Δ=(2m−1)² |x₁−x₂|=3⇔

	−b−√Δ		−b+√Δ
|		−		|=3⇔
	2a		2a

	√Δ
|		|=3
	2

|2m−1|=6 dokonczcie.

zawodus: czyli masz dobrze

Marcin: 2m−1=6 2m=7

	7
m=
	2

2m−1=−6 2m=−5

	−5
m=
	2

Marcin: Pani Milu wyniki identyczne, ale obliczeń 100 razy mniej

maturzysta14: zadania od Bogdana KOSMOS

Mila:

Piotr 10: Ja to myślę, że tak: Oblicz najmniejszą wartość wielomianu: (x−1)*(x−2)*(x−3)*(x−4)+4 (x−1)*(x−4) *(x−2)*(x−3)+4= [x²−5x+4] * [(x²−5x+4)+2]+4=(x²−5x+4)²+2(x²−5x+4)+4= (x²−5x+4)²+2x² −10x+12 Najmniejsza wartość będzie wtedy, gdy: x²−5x+4=0 Δ=25−16=9 √Δ=3 x₁=4 v x₂=1 oraz gdy: 2x²−10x+12=f(x)

	10
xw=		=2,5
	4

f(1)=2−10+12=4 f(4)=2*16−10*4+12=4 coś tu nie gra, zaraz wracam

Mila: I o to chodzi Marcin.

Marcin: 5−latek, ta moja propozycja, to będzie wysokość drugiego wielościanu ma się rozumieć, tak?

Marcin: A nie. Wysokość drugiego to po prostu a

5-latek: Marcin . Teraz tak . oznaczyny objetosc graniastoslupa przez V , V₁ −obj czesci dolnej i V₂ obj. czesci gornej

	V1
My musimy poszukac stosunku k=
	V2

V₁ policzyc latwo ale V₂ bedzie juz trudno (bo bedzie to graniastoslup ukosnie sciety ) Dlatego wez sobie przeksztalc ten stosunek k tak

1		V2		1		V2		k+1		V
	=		stad mamy		+1=		+1 stad		=
k		V1		k		V1		k		V1

Teraz dzialaj juz dalej sam

Marcin:

	3a3tgα
V1 =
	24

	a3√3
V2 =
	12

Stosunek:

3a3tgα		12		√3tgα
	*		⇒
24		a3√3		2

Marcin: ahh no tak, to nie jest po prostu ostrosłup

maturzysta14: 5 latek w twoim rownaniu powinienem dojść do sinx+cosx=0 ?

Piotr 10: Ja dokończę swoje rozwiązanie z wielomianem jutro, teraz idę

5-latek: A co bedzie 1 wieloscianem ?

Marcin: 1 wielościan to ostrosłup z trójkątem równobocznym w podstawie

5-latek: Maturzysta 14 Tak jak piszsesz 20:25

5-latek: Wylicz teraz V i V₁

maturzysta14: poprosze o kolejne zadania, stereometrie jeszcze nie powtarzałem także odpuszczam narazie zadania tego typu.

zombi: ICSP podpowiedź jakaś?

maturzysta14: też porposzę !

Marcin: 5−latek

	a3√3
V=
	12

	3a3tgα
V1=
	24

Podstawiając to do tego wzoru wychodzi trochę obliczeń (w których zapewne się pomyliłem), ale

	−6tgα
k=
	2√3−3tgα

maturzysta14: https://matematykaszkolna.pl/forum/198720.html to znalazłem, całe rozwiązanie.

5-latek: Maturzysta 14 masz nastepne . W plaszczyznie trojkata rownobocznego ABC o boku dlugosi a znalezc pole obszaru zawierajacego takie i tylko takie punkty M ze a) kąty AMB, BMC, CMA sa rozwarte B) kąty AMB i BMc sa zawarte w przedziale <60 :,90> stopni .

zombi: Aaaa czyli jednak dobrze kombinowałem z modulo, a później z iloczynową.

maturzysta14: 5−latek nie wiem jak sie za to zabrać ale po zrobieniu rysunku w a) na pewno na wysokości poprowadzonej do podstwy a dokładniej na 1/3 h, tylko nie wiem z czego zupełnie to wynika

5-latek:

	a3√3
Marcin V=		przeciez wysokosc graniastoslupa jest a
	4

	a3
V1 po uproszceniu =		tgx
	8

	k+1		V
Stosunek		=		= 2√3ctgx
	k		V1

	1
wiec k=		= (2√3ctgx−1)−1
	2√3ctgx−1

Teraz wniosek Stosunek ten nie zalezy od dlugosci krawedzi

	2√3
Tez z warunku ze h<a wynika tez ze 0<tgx<
	3

Marcin:

	1
Bo ja to policzyłem jako dla ostrosłupa, czyli jeszcze pomnożyłem przez		, ciamajda ze
	3

mnie na potęgę

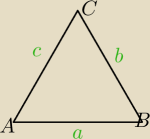
5-latek: POdpowiedz do a)

	a
Teraz jesli ze srodka odcinka AB zatoczysz luk o promieniu r=		to zuwaz ze wnetrze
	2

powstalego kola bedzie zbiorem punktow spelniajacym warunek kąt AMB >90 stopni Powtorz tak samo dla boku BC i AC Zobaczysz jak figure otrzymasz

5-latek: Marcin Wbrew pozorom to bylo trudne zadanie . Wymagalo myslenia . Masz nastepne zadanie Kat ostry rownolegloboku wynosi 45 stopni Punkt wsppolny przekatnych rownolegloboku oddalony jest od bokow o 2√2i 2 Oblicz pole rownolegloboku i dlugosci przekatnych

Marcin: Jak to wbrew pozorom? Po prostu było trudne

Marcin: Coś takiego co do tego zadania 1?

5-latek: Jeszce jedno dzisiaj i juz koniec z zadaniami OK? Rozwiaz uklad rownan {x²−5y²+4=0 {log₄x−log₂y=0

5-latek: Post 21:31 . tak tylko zauwaz ze to zakreskowane pole = polu trojkata rownobocznego i 3 pol jednakowych odcinkow kola .

	a2
Mam odpowiedzi do tego zadania i do a) Pole =		(pi−√3)
	8

	a2
Do b)		(2pi+3√3)
	72

Marcin: W tym w równoległobokiem będzie P=32, a przekątne 4√2 i 4√10

5-latek: Tak ale dobrze by bylo gdybys przedstawil obliczenia . Nie musisz dzisiaj . Moze jeszce ktos skorzysta

Marcin: Nie fajnie że nie potrafię tutaj rysować, bo zobrazowałbym swój sposób Wysokość tego równoległoboku to musi być 4, bo to po prostu 2*2, a 2 to odległość do do jednego z boków. Później już trzeba wyliczyć podstawę, także to już z funkcji trygonometrycznych Mamy oczywiście 4√2 jako bok b(przekątna kwadratu) 2*nasza druga odległość, da nam przeciwprostokątną trójkąta z którego obliczymy podstawę.

	4√2
sin45=		⇒ Podstawa = 8
	x

Pole to 8*4=32 Przekątne to już tylko 2* pitagoras

Saizou : ICSP może jakaś podpowiedź do tego Twojego zadanka

Marcin: Saizou zobacz tutaj rozwiązanie Bizona https://matematykaszkolna.pl/forum/198720.html

Saizou : cóż właśnie coś takiego kombinowałem x wzorem (a+b+c)² ale jakoś nie wyszło

maturzysta14: poprosze o kolejną dawke zadan!

zawodus: Jakiego typu?

maturzysta14: maturalnego

zawodus: dobra, ale założę inny temat.