matematykaszkolna.pl
Road to matura exam Saizou : Road to matura exam zad1/ Wykaż jeżeli liczba x jest całkowita nieparzysta, to liczba: x6−x4−x2+1 jest podzielna przez 32 zad2/ Wykaż ,że suma kwadratów trzech kolejnych liczb całkowitych, z których najmniejsza jest postaci 2n−3 ,n∊C z dzielenia przez 3 daje resztę 2
2 lut 20:07
Saizou : to zaczynamy drogę xd zad 1 x=2k−1 k∊C dowód: x6−x4−x2+1 = x2(x4−1)−1(x4−1)= (x4−1)(x2−1)= (x2−1)2(x2+1)= (x−1)2(x+1)2(x2+1)= (2k−1−1)2(2k−1+1)2(4k2−4k+1+1)= 4(k2−2k+1)4k22(2k2−2k+1)= 32k2(k2−2k+1)(2k2−2k+1)=32t, t∊C ckd
2 lut 20:12
Piotr 10: 2. 2n−3 , 2n−2 , 2n−1 (2n−3)2+(2n−2)2+(2n−1)2=4n2 −12n+9+4n2 − 8n+4+4n2 −4n+1=12n2−24n+14)= =3(4n2 − 8n+4)+2 xD
2 lut 20:15
Saizou : zad2 (2n−3)2+(2n−2)2+(2n−1)2= 4n2−12n+9+4n2−8n+4+4n2−4n+1= 12n2−24n+12+2= 3(4n2−8n+4)+2
2 lut 20:15
Eta: zad.3/ W trapezie ABCD :AB∥CD i |AB|=a, |CD|=b i a>b oraz suma kątów ostrych jest równa 90o.
 a−b 
Wykaż,że długość odcinka łączącego środki podstaw trapezu ma długość
 2 
2 lut 20:18
Marcin: Drugie też zrobiłem. jeee emotka
2 lut 20:19
Eta: zad.4/ Oblicz pole trapezu, w którym suma kątów ostrych = 90o zaś różnica kwadratów przekątnych jest równa 16
2 lut 20:21
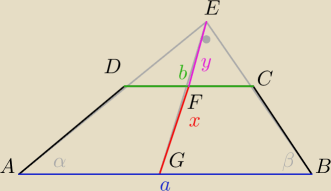
Saizou : rysunek ΔCEF~ΔAEF
y y+x 
=
1 
b
2 
 
1 
a
2 
 
2y 2y+2x 
=
b a 
2ya=2yb+2xb 2xb=2ya−2yb xb=ya−yb
 ya−by y(a−b) 
x=
=
"a dalej muszę coś pokombinować xd
 b b 
2 lut 20:36
Marcin: Saizou, czyli Ciebie też można na czymś zatrzymać
2 lut 20:37
Marcin: Brawa dla Pani Ety emotka
2 lut 20:38
Saizou : nigdy nie lubiłem geometrii
2 lut 20:39
Marcin: Ja nigdy nie lubiłem zadań dowodowych, a większość od Ciebie taka była
2 lut 20:39
Saizou : no widzisz emotka
2 lut 20:40
5-latek: Marcin nie przejmuj sie tym . Kiedys Saizou nie chcial rozwiazywac zadan ode mnie bo powiedzial ze zbyt opisowe emotka
2 lut 20:47
Mila: A tu ładne zadania są. Pozdrawiam uczących i uczących się. emotka
2 lut 20:58
Marcin: Ja się nie przejmuję. Przejmować się będę w maju emotka
2 lut 21:00
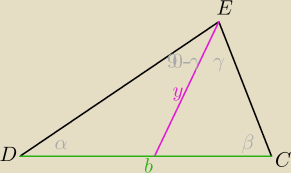
Saizou : rysunek
y 
1 
b
2 
 
=
sinα sin(90−γ) 
y 
1 
b
2 
 
=
sin(90−α) sinγ 
łącząc to wyjdzie że α=γ, zatem
 1 
y=
b
 2 
2y=b wrzucając to do
 y(a−b) y(a−b) a−b 
x=
=
=
 b 2y 2 
2 lut 21:07
Eta: @ Saizou Zauważ okręgi opisane na trójkątach prostokątnych......... R= .....
2 lut 21:32
Saizou : na to samo wyjdzie emotka
2 lut 21:43
Eta: emotka
2 lut 21:51
Eta: No to zostało jeszcze zad.4 emotka
2 lut 21:53
Eta: emotka
2 lut 22:35
Saizou : I still thinking emotka
2 lut 22:38
Ajtek: A ja wiem, że 2+2 jest 4
3 lut 01:59
Saizou : totalne bzdury mi tu wychodzą emotka
3 lut 22:11
Eta: Sorry (pomyliłam dane ) .... w treści ma być ,że kąty ostre to 30o i 60o Teraz działaj emotka
3 lut 22:13
Saizou : to wiele pomoże, bo mi coś zawsze zostawało i nic nie wychodziło
3 lut 22:14
Eta:
3 lut 22:15
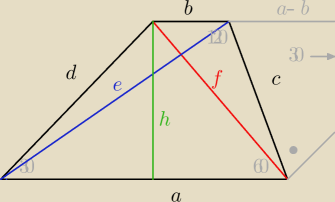
Saizou : rysunek e>f e2=a2+c2−ac f2=b2+c2+bc −−−−−−−−−−−−−−−−−−−−−− 16=a2−b2−ca−bc 16=(a−b)(a+b)−c(a+b) 16=(a+b)(a−b−c)
 h 2√3 
sin60=
→c=
h
 c 3 
 a−b 
sin60=
→h=a−b
 c 
 3−2√3 
16=(a+b)(
h)
 3 
46 
=(a+b)h
3−2√3 
23(3+2√3) (a+b)h 
=
9−12 2 
fajnie że pole wyszło mi ujemne emotka
3 lut 23:21
Eta:
3 lut 23:22
Saizou : tylko gdzie błąd emotka
3 lut 23:22
Saizou : już wiem
 c 
sin 60=
emotka
 a−b 
3 lut 23:23
Saizou : czyli po poprawkach mamy P=12(2−√3) emotka
3 lut 23:26
Eta: https://matematykaszkolna.pl/forum/208455.html 22 lipca rozwiązywał niejaki Saizou znasz Go ? emotka
3 lut 23:29
Saizou : hehe pomyśleć że to byłem ja, no nic muszę szukać błędu w moim rozwiązaniu
3 lut 23:32
Saizou : Eta a mogłabyś mi pomóc znaleźć błąd ?
3 lut 23:40
Eta:
a−b 
= cos60o
c 
4 lut 00:12
Saizou: faktycznie, poprawie rano bo juz ide spac, kolorowych snow
4 lut 00:14
Eta: Miłych snów emotka nie tylko o trapezach emotka
4 lut 00:16
Saizou : no i teraz wyszło wszystko P=4√3
4 lut 10:20
Saizou : Eto masz coś jeszcze ? emotka
4 lut 22:07
Eta: Mam .... dobrą pigwówkę
4 lut 22:09
Saizou : hehe rozpijasz młodych ludzi emotka
4 lut 22:10
Eta: Wykaż,że jeżeli równanie : x4+ax2+b=0 ma cztery różne pierwiastki tworzące ciąg arytmetyczny, to 9a2=100b
4 lut 22:12
Saizou : czy te pierwiastki to same zera?
4 lut 22:23
Saizou : nie było pytanie emotka
4 lut 22:24
Eta: Jak czytasz treść? : "ma cztery różne pierwiastki" emotka
4 lut 22:24
zombi: emotka
4 lut 22:25
Eta: Co zombi ?emotka
4 lut 22:26
zombi: −3,−1,1,3
4 lut 22:27
Saizou : ufff... upiekło mi się
4 lut 22:27
Saizou : Zał: W(x)=x4+ax2+b=0 ma 4 pierwiastki Teza: 9a2=100b Dowód: W(x)=(x−d)(x−e)(x−f)(x−g) W(x)=x4+(−g−f−e−d)x3+(fg+eg+ef+dg+df+de)x2+(efg−dfg−deg)x+defg −g−f−e−d=0 →e+d+f+g=0 fg+eg+ef+dg+df+de=a efg−dfg−deg=0 defg =b i to trzeba rozwiązać, czy jest jakiś inny sposób ?
4 lut 22:38
Saizou : no to pora wykorzystać info że tworzą ciąg
4 lut 22:39
zombi: zamiast 4 literek zrób po dwie, bo skoro x4+ax2+b=0 ma 4 pierwiastki to wygląda tak (x2−t2)(x2−p2)
4 lut 22:41
zombi: Poza tym zastanów się jak mogą wyglądać takie ciągi. Wiesz, że ma pierwiastki −t, −p, p, t w tej kolejności rosnącej. Znajdź taki przykładowy ciąg, który to spełnia.
4 lut 22:47
Saizou : d=x−r→d=3x e=x f=x+r →f=−x g=x+2r →g=−3x ===========+ d+e+f+g=4x+2r=0→2x+r=0→r=−2x defg=3x*x*(−x)(−3x)=9x4=b /*100→900x4=100b fg+eg+ef+dg+df+de=a→10x2=a /2→100x4=a2/*9→900x4=9a2 9a2=100b ckd
4 lut 22:50
Saizou : zombi dzięki nawet tak nie pomyślałem xd, przez co pojechałem na ferie przez Rosję, Kanadę, Włochy, Austrię, Szwajcarię i wiele innych krajów xd
4 lut 22:58
Eta:
4 lut 23:00
Saizou : ale się udało
4 lut 23:01
Eta: emotka emotka
4 lut 23:02
Saizou : można prosić o kolejne zadanko ?
4 lut 23:03
5-latek:
 1 
Dla jakich wartosci x z przedzialu <0,pi> spelniona jest nierownosc √cosx−sinx≥six−
 2 
4 lut 23:10
Saizou :
 1 
tam jest sin(x)−
 2 
4 lut 23:13
5-latek:
 1 
≥sinx−
zjadlem n emotka
 2 
4 lut 23:17
Saizou :
 π 
to jest prawdziwe tylko dla x∊<0
> emotka
 4 
4 lut 23:19
Saizou : sorry nie tę wartość podstawiłem
4 lut 23:22
5-latek: masz jeszce jedno i ide juz emotka
 1 
log1/2sin2xsinx=
 2 
 1 
W podstawie logarytmu jest
sin2x
 2 
4 lut 23:22
Saizou :
 1 
√cosx−sinx≥sinx−
 2 
zał
 π 
cosx≥sinx→x∊<0:
>
 4 
 1 π 5 
sinx≥
→x∊<
:
π>
 2 6 6 
 π π 
łącząc fakty mamy że x∊<
:
>
 6 4 
 1 
√cosx−sinx≥sinx−
/2 bo L i P≥0
 2 
 1 
cosx−sinx≥sin2x−sinx+
 4 
 1 
cosx≥sin2x+
 4 
 1 
cosx≥1−cos2x+
 4 
4cos2x+cosx−3≥0 4t2+t−3≥0 Δ=49
 3 
t=
t=1
 4 
 3 
t≥
i t≤−1
 4 
 3 
cosx≥
cosx≤−1 (istnieje opcja tylko cosx=−1 co i tak nie będzie spełniać warunków
 4 
zadania)
 3 
no i teraz nie wiem jak obliczyć cosx≥
 4 
4 lut 23:32
Saizou : Miłych snów emotka
4 lut 23:33
Saizou : już wiem gdzie mam bład emotka
4 lut 23:34
Saizou : jutro policzę a teraz letę spać, cześc xd
4 lut 23:37
Saizou :
 1 
√cosx−sinx≥sinx−
 2 
.... 4cos2x+4cosx−5≥0 (2cosx+1−√6)(2cosx+1+√6)≥0 uzyskamy
√6−1 
≤cosx≤1
2 
no i teraz nie wiem
5 lut 09:40
Saizou :
 π 
a z logarytmem wyjdzie że x=
+2kπ , k∊C
 4 
5 lut 10:00
zawodus: wynik wychodzi w tym zadaniu nieładny...
5 lut 10:01
Saizou : mówisz o nierówności ?
5 lut 10:04
wredulus_pospolitus:
 √6−1 √2 
a najgorsze jest to, że
>
 2 2 
ale pomijając na chwilę tę kwestię ... Saizou −−− ale to nie koniec zadania ... Twoje drugie założenie to jest założenie do 'podpunktu' w końcu sinx−0,5 może być <0 (kto mu broni )
5 lut 10:04
Saizou : dlatego to nie koniec zadanie
5 lut 10:11
ZKS:
 π 
Saizou a co otrzymasz jeżeli x ∊ [0 ;
]? emotka
 6 
5 lut 10:42
Saizou : uzyskamy zawsze prawdę xd
5 lut 13:40
5-latek: zadanie z logarytmem taka tez mam odpowiedz
 √6−1 
Zadnie z nierownoscia . Mam taka odpowiedz 0≤x≤arc cos
 2 
5 lut 16:38
zawodus: 5−latek tylko, że maturzyście często nie wiedzą co to arccosx
5 lut 16:39
zawodus: A na pewno na maturze się nie pojawi takie zadanie
5 lut 16:40
5-latek: No to jak zrobisz tamto zadanie to jeszce jedno rownanko trygonometryczne i starczy emotka
 3 π−α 
ROzwiaz rownanie 2sin(
π−α)+√3tg
=2
 2 2 
5 lut 16:46
5-latek: czesc. Ale Saizou wie co to jest emotka Podejrzewam ze bedzie tak jak mowisz ze sie nie pojawi na maturze ale niech saizou sprobuje rozwiazac ,. Nie zaszkodzi
5 lut 16:49
5-latek: Zadanka pochodza ze zbioru zadan z matematyki elementarnej Aniela Ehrenfeucht , Olga Stande z 1975r.
5 lut 16:52
zawodus: Sam muszę się zaopatrzyć w stare podręczniki i zbiorki emotka Mam obecnie kilka, ale to wciąż za mało
5 lut 16:56
5-latek: Powiem CI ze ten jest zarabisty to byla algebra A drugi to Zbior zdan z matematyki elementarnej −geometria Stanislaw Serafin, Gustaw Trelinski
5 lut 17:01
5-latek: Zamowilem je sobie zeby mi przypominaly moje lata szkolne emotka
5 lut 17:02
zawodus: widzę go na allegro emotka może uda mi się upolować emotka
5 lut 17:02
5-latek: Ja CI go nie sprzatne emotka
5 lut 17:04
zawodus: Teraz jak będę miał chwilkę po antykwariatach pochodzę. emotka W końcu na coś trzeba kasę z korków wydawać
5 lut 17:05
5-latek: A narzeczona Cie nic nie kosztuje ze nie masz na co kasy wydawac ?)))) POza tym kup sobie od czasu do czasu dobra flaszke emotka
5 lut 17:08
5-latek: Ja jutro jade ze swoja wnuczka do krawcowej zeby jej uszyla stroj konika pony . tak sobie umysllila i kasa pojdzie emotka
5 lut 17:10
zawodus: 5−latek narzeczona kosztowała, ale na żonie to próbuje zaoszczędzić (z marnym skutkiem) emotka
5 lut 17:15
5-latek: Wiem ze tak jest. sam to przeszedlem emotka
5 lut 17:20
5-latek: Zawodus . Znamy to . KOchanie nie mam w co sie ubrac emotka
5 lut 17:21
zawodus: Pomimo pełnej szafy oraz tekst: kochanie, ale w tym mnie już widzieliemotka muszę mieć coś innego I wtedy twoje krążenie się poprawia
5 lut 17:23
5-latek: Dobreemotka
5 lut 17:24
zawodus: Zależy z czyjej perspektywy
5 lut 17:28
Saizou : arccosx to funkcja odwrotna o cosx w kalkulatorach często zapisywana jako cos−1
5 lut 20:53
5-latek:
 1 2 
Odpowiedz do zadania 16:46 jest taka α=
π+2kπ lub α=
π+2kπ lub α=(2k+1)π
 3 3 
Jesli zechcesz je rozwiazac emotka
5 lut 21:09
Saizou :
 1 π 1 π 
2sin(270−x)+√3tg(90−
x)=2 zał
−
x≠
+kπ→x≠−2kπ
 2 2 2 2 
 1 1 
−2cosx+√3ctg(
x)=2
x=t
 2 2 
 1 
−2cos(2t)+√3ctg(t)=2 zał
x≠kπ→x≠2kπ k∊C
 2 
−2(cos2t−sin2t)+√3ctg(t)=2
 cost 
−2(2cos2t−1)+√3
=2
 sint 
 cost 
−4cos2t+2+√3
=2
 sint 
 √3 
cost(−4cost+
)=0
 sint 
 π 1 
cost=0→
+kπ=
x→x=π+2kπ spełnia założenia
 2 2 
 √3 
−4cost+
=0
 sint 
−4sintcost+√3=0
 √3 
2sintcost=
 2 
 √3 π 2 
sin(x)=
→x=
+2kπ lub x=
π+2kπ te rozwiązania też
 2 3 3 
spełniają założenia
5 lut 21:19
Saizou : emotka
5 lut 21:20
5-latek: Jutro po pracy wstawie swoje rozwiazanie OK? teraz spanie bo o 5:30 trzeba wstawac emotka
5 lut 23:08
Saizou : ok, kolorowych snów emotka
5 lut 23:09
5-latek: OK. za α wstawie x Rownanie to ma sens dla x≠ 2kpi
 pi−x 3 
 1 
1−tg2
x
 2 
 
tg
=ctg{x}{2} sin(
pi−x)=−cos x =−
dla x nie
 2 2 
 1 
1+tg2
x
 2 
 
rowna sie (2k+1)pi teraz 1. dla x nie rowna sie (2k+1)pi mam
 
 1 
1−tg2
x
 2 
 √3 1 1 
−2
+
=2⇔(tg
x=
llub
 
 1 
1+tg2
x
 2 
 
 1 
tg
x
 2 
 2 √3 
 1 1 2 
tg
x=√3)⇔(x=
pi+2kpi lub x=
pi+2kpi)
 2 3 3 
2. dla x=(2k+1)pi rownanie jest spelnione
6 lut 18:10
Saizou : emotka
6 lut 21:45
5-latek: Zadanko z e zbioru zadan Drobka Szymanski dla klasy 3 i 4 liceum .Wykaz z edla kazdego x∊R
 1 
spelniona jest nierownosc sin6x+cos6x≥
 4 
6 lut 22:12
zombi: Ja też mogę czy tylko Saizou? emotka
6 lut 22:21
Saizou : z nierówności o średnich potęgowych mamy
 sin6x+cos6x sin2x+cos2x 
6√
≥2√
/6
 2 2 
 1 
sin6x+cos6x≥
 4 
6 lut 22:22
zombi: No i uprzedził mnie
6 lut 22:23
5-latek: Moze jeszce troche poczekaj . Jak sie nie odezwie to mozesz emotka
6 lut 22:23
Saizou : zombi tak z ciekawości, przygotowywałeś się do olimpiady z matematyki ?
6 lut 22:26
zombi: Kiedyś tak, Pawłowskiego przerobiłem dwie książki + zadania z om.edu.pl i peeełno innych konkursowych, ale ze znikomym skutkiem niestety : (
6 lut 22:34
Saizou : właśnie widać po Twoich rozwiązaniach że "liznąłeś" olimpijskiej matematyki
6 lut 22:35
5-latek: ja rozwiazalem to tak =(sin2x)3+(cos2x)3=(sin2x+cos2x)(sin4x−sin2xcos2x+cos4x)=(1−cos2x )2−(1−cos2x)cos2x+cos4x=3cos4x−3cos2x+1
 1 
Jesli teraz wezniemy pod uwage funkcje g(x)=3cos4x−3cos2x+1 i funkcje h(x)=g(x)−
to
 4 
 1 
h(x)= 3cos4x−3cos2x+1−
=3cos4x−3cos2x+U{3}{4]=3(cos4x−cos2x+U{1}
 4 
 1 
{4})=3(cos2x−
)2
 2 
 1 
wiec tak h(x)>=0 dla kazdego x nalezacego do R czyli g(x)−
>=0 stad mamy z e
 4 
 1 
g(x)>=
 4 
6 lut 22:43
Saizou : emotka
6 lut 22:46
5-latek: MOze juz jutro znajde jakies ciekawe 2 ,3 zadankaemotka .
6 lut 22:49
Saizou : no to za trochę więcej niż godzinę emotka
6 lut 22:51
5-latek: Mialem na mysli jutro po pracy emotka
6 lut 22:52
Saizou : no chyba że....
6 lut 22:53
5-latek: To napisz z jakiego dzialu a jutro jak spojrze w post to bede wiedzial co szukac . Dobrze ?
6 lut 22:55
Saizou : planimetria
6 lut 22:56