.
bezendu:
Bryły.
1 lut 16:08
Mila:
1) Oblicz V i Pc graniastosłupa prawidłowego trójkątnego o krawędzi podstawy a=20 cm i
wysokości H=10 cm. Zaznacz kąt między przekątną ściany bocznej i sąsiednią ścianą boczną.
(rysunek)
2) Oblicz V i Pb graniastosłupa prostego, którego podstawą jest trójkąt prostokątny o
przyprostokątnych 3 cm i 4 cm, wiedząc, że długość przekątnej ściany boćznej zawierającej
przeciwprostokątną podstawy jest równa 15 cm. (rysunek)
3) Przekątna sześcianu jest o 1 cm dłuższa od jego krawędzi.
Oblicz Pc sześcianu . ( bez rysunku)
Będę po 20. Powodzenia.
1 lut 16:20
5-latek:
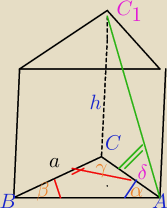
podstawa graniastoslupa prostego jest trojkat ABC w ktorym dany jest bok a oraz dwa katy β i γ
przylegle do tego boku . Przekatna sciany bocznej na ktorej lezy bok AC jest nachylona do
tego boku pod katem δ. Oblicz objetosc graniastoslupa
1 lut 16:28
bezendu:
3, a
√3=a+1
a
√3−a=1
a(
√3−1}=1
P
c=6a
2
P
c=6+3
√3
1 lut 16:39
bezendu:
1.
a=20cm
H=10cm
P
p=100
√3cm
2
V=100
√3*10
V=1000
√3cm
3
P
b=3*(10*20)
P
b=600cm
2
P
c=2P
p+P
b
P
c=200
√3+600
P
c=200(
√3+3)cm
2
1 lut 17:15
bezendu:
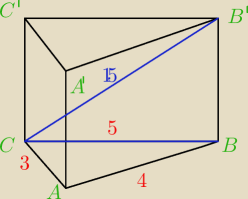
1.
h−wysokość w trójkącie prostokątnym
H−wysokość graniastosłupa
P
p=6
|BB'|=15
2−5
2
|BB'|=10
√2
V=6*10
√2=60
√2
P
b=4*10
√2+3*10
√2+5*10
√2
P
b=40
√2+30
√2+50
√2
P
b=120
√2
1 lut 17:32
Mila:
3) Dobrze.
Rada:
a(
√3−1)=1 /(
√3+1)
a*(3−1)=
√3+1
2) Kąt , zobacz u
Marcina, tam narysowałam.
dalej sprawdzam.
1 lut 20:53
1 lut 20:57
Mila:
2) Lepiej pole trójkąta prostokatnego tak:
P
b=(a+b+c)*H
P
b=(3+4+5)*10
√2
P
b=120
√2cm
2
Jeśli w zadaniu podane jednostki, to końcowe wyniki podawaj z jednostkami.
1 lut 21:00
Mila:
20:57 Tak.
1 lut 21:02
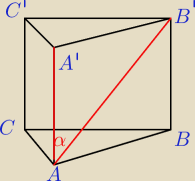
Mila: 4)
W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej jest równe sumie pół obu
podstaw.
Oblicz cosinus kąta nacylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej.
(najpierw tylko rysunek z oznaczeniami wierzchołków)
1 lut 21:03
bezendu:
| | ab | |
Ja korzystałem z tego wzoru h= |
| wysokość poprowadzona na przeciwprostokątną  |
| | c | |
Dobrze, zapamiętam uwagę.

1 lut 21:04
bezendu:
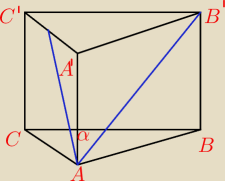
1 lut 21:07
Mila:
U góry brak w górnej podstawie odcinka łączącego punkt D z B'.
Rysuj jeszcze raz . To wazne zadanie.
1 lut 21:13
bezendu:
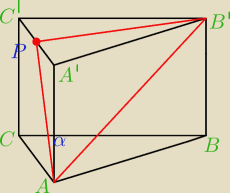
1 lut 21:18
bezendu: Tylko czemu nie rozumiem jednego czemu AP jest pod kątem prostym ?
1 lut 21:38
Mila:
Bardzo dobrze.
Teraz licz.
1 lut 21:39
Mila:
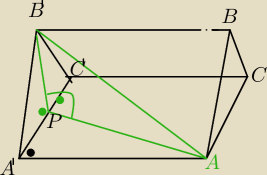
B'P⊥A'C'
rzutujesz AB' na płaszczyznę ACA'C', to jets rzut prostopadły.
AP⊥PB' z tw. prosta B'P przebija płaszczyznę ACA'C', to jest prostopadła do każdej prostej z
tej płaszczyzny przechodzącej przez punkt przebicia.
1 lut 21:53
1 lut 21:55
bezendu: ?
1 lut 22:15
bezendu:
Ja już muszę dziś kończyć. Wrócę juto do tego zadania. Dziękuję za pomoc i dobranoc

Niech nikt nie rozwiązuję za mnie.
1 lut 22:30
Mila:
Zrozumiałeś ten kąt?
1 lut 22:35
bezendu:
Tak, ale na prawdę już muszę iść. Dziękuję jeszcze raz za pomoc bo już coraz więcej rozumiem.
1 lut 22:37
2 lut 12:52
52: Trochę się wtrącę ...
Może ktoś narysować kąt zawarty między sąsiednimi ścianami bocznymi ostrosłupa prawidłowego
czworokątnego?
2 lut 14:35
kika:
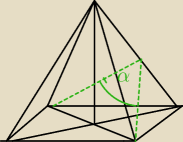
2 lut 14:52
52: Dzięki

2 lut 14:55
Mila:
Czekam. PB' nie może być tak wyrażone− 12:52.
2 lut 14:58
bezendu:
Robię od początku:
6aH=a
2√3
Przekątna ściany bocznej−k
cosα=57
0
2 lut 16:35
Mila: Do rys. 21:18
| | a√3 | | 1 | | 1 | |
AP2=( |
| )2+ |
| a2= |
| a2 |
| | 6 | | 4 | | 3 | |
2 lut 17:12
bezendu:
To który odcinek źle wyznaczyłem ?
2 lut 17:13
Mila:
k2 masz dobrze, k źle .
2 lut 17:25
bezendu:
Już wiem gdzie błąd. A tamte poprzednie zadania są ok ?
2 lut 17:27
Mila:
Tak, pisałam.
2 lut 17:30
bezendu: To mogę prosić o kolejne ?
2 lut 17:32
Mila: W nowym wątku, dobrze?
2 lut 17:35
bezendu: Dobrze, już zakładam.
2 lut 17:36
 podstawa graniastoslupa prostego jest trojkat ABC w ktorym dany jest bok a oraz dwa katy β i γ
przylegle do tego boku . Przekatna sciany bocznej na ktorej lezy bok AC jest nachylona do
tego boku pod katem δ. Oblicz objetosc graniastoslupa
podstawa graniastoslupa prostego jest trojkat ABC w ktorym dany jest bok a oraz dwa katy β i γ
przylegle do tego boku . Przekatna sciany bocznej na ktorej lezy bok AC jest nachylona do
tego boku pod katem δ. Oblicz objetosc graniastoslupa
 1.
a=20cm
H=10cm
1.
a=20cm
H=10cm
 1.
h−wysokość w trójkącie prostokątnym
H−wysokość graniastosłupa
1.
h−wysokość w trójkącie prostokątnym
H−wysokość graniastosłupa




 B'P⊥A'C'
rzutujesz AB' na płaszczyznę ACA'C', to jets rzut prostopadły.
AP⊥PB' z tw. prosta B'P przebija płaszczyznę ACA'C', to jest prostopadła do każdej prostej z
tej płaszczyzny przechodzącej przez punkt przebicia.
B'P⊥A'C'
rzutujesz AB' na płaszczyznę ACA'C', to jets rzut prostopadły.
AP⊥PB' z tw. prosta B'P przebija płaszczyznę ACA'C', to jest prostopadła do każdej prostej z
tej płaszczyzny przechodzącej przez punkt przebicia.
 Niech nikt nie rozwiązuję za mnie.
Niech nikt nie rozwiązuję za mnie.

