Marcin: Czekam na jakieś ciekawe zadanie od Pani Mili emotka

31 sty 22:15

Saizou : to tak na rozgrzewkę zad 1 Niech A i B będą zdarzeniami losowymi zawartymi w Ω. Wykaż że jeśli P(A)=0,7, P(B)=0,4 to 0,1≤P(A∩B)≤0,4

31 sty 22:19

Saizou : zad. 2 Udowodni że dla dowolnych licz dodatnich a i b prawdziwa jest nierówność

√a²+1		√b²+1		1		1
	*		≥		+
a		b		a		b

31 sty 22:22

bezendu: Widzę zielony Aksjomat leci emotka

31 sty 22:24

Saizou : zad. 3 W równoległoboku kąt ostry ma miarę 60^o. Oblicz stosunek długości boków równoległoboku, jeżeli

	19
stosunek kwadratów długości jego przekątnych jest równy
	7

31 sty 22:26

Saizou : a tak jakoś był pod ręką xd

31 sty 22:26

Saizou : zad. 4

	π		π
Wykaż że funkcja f(x)=cos²x+cos²(		+x)−cosxcos(		+x) jest funkcją stałą
	3		3

31 sty 22:29

Mila: W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej jest równe sumie pół obu podstaw. Oblicz cosinus kąta nacylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej. (najpierw tylko rysunek z oznaczeniami wierzchołków)

31 sty 22:29

Saizou : zad. 5 Wykaż, że wielomian (x+1)(x+2)(x+3)(x+4)+1 można przedstawić w postaci kwadratu trójmianu kwadratowego

31 sty 22:34

Marcin: Ok. Chwile mnie nie było, ale wracam. Dzięki za zadania, jakoś spróbuję się ich podjąć emotka

31 sty 22:45

Marcin: P(A∩B) = 1,1 −P(AUB) P(A∩B) maksymalnie może być równe 1 Czyli P(AUB) ≥0,1, dobrze myślę?

31 sty 22:55

Saizou : dobrze myślisz

a teraz pokaż jeszcze ograniczenie że P(A∩B)≤0,4

31 sty 22:57

Piotr 10: Niech A i B będą zdarzeniami losowymi zawartymi w Ω. Wykaż że jeśli P(A)=0,7, P(B)=0,4 to 0,1≤P(A∩B)≤0,4 P(A ∪ B)=P(A)+P(B) − P(A∩B) 0≤P(A ∪ B) ≤ 1 0 ≤P(A)+P(B) − P(A∩B)≤1 0 ≤0,7+0,4 − P(A∩B) ≤ 1 0≤1,1 − P(A∩B) ≤ 1 0≤1,1 − P(A∩B) i 1,1 − P(A∩B) ≤ 1 P(A∩B) ≤ 1,1 i P(A∩B) ≥ 0,1 1,1 ≥ 0,4 Więc P(A∩B) ≤0,4 i P(A∩B) ≥ 0,1 Można tak ?

31 sty 23:05

Marcin: No skoro P(B)=0,4, to jasne jest, że cześć wspólna tych zdarzeń nie może być większa.

31 sty 23:08

Saizou : i w tym momencie dostajesz 0 ptk, bo napisałeś że P(A∩B)>1 emotka

a odpowiedź jest znacznie prostsza

31 sty 23:08

Saizou : Marcin dobrze

, czyli wystarczy napisać że P(A∩B)≤P(B)=0,4 zatem 0,1≤P(A∩B)≤0,4

31 sty 23:10

Marcin: No tak. Ja to chciałem 'ubrać' w słowa emotka

31 sty 23:11

Saizou : a po co matematyka to język symboli xd

31 sty 23:12

Marcin: Chciałem żebyś zrozumiał mój tok myślenia. Biorę się za 2 emotka

31 sty 23:13

Saizou : ja muszę lecieć, na pewno ktoś sprawdzi, a jak nie to się jutro upomnij xd

31 sty 23:29

Marcin: ehh szkoda. emotka

31 sty 23:29

bezendu: @Marcin zrobiłeś to 2 ?

31 sty 23:29

Marcin: Tak, zrobiłem, ale nie mam pewności czy dobrze. Przepisać?

31 sty 23:31

Saizou : napisz to jeszcze sprawdzę xd

31 sty 23:31

Marcin: Podnoszę to do kwadratu obustronnie, później przenoszę, redukuje i zwijam we wzór skróconego mnożenia. Taki schemat ma być? emotka

31 sty 23:41

Piotr 10: możesz od razu pomnożyć przez ab bo a > 0 i b >0 czyli a*b > 0

31 sty 23:42

Marcin:

	1
Mam na końcu (1−		)²≥0
	ab

31 sty 23:42

Saizou : emotka

i bardzo dobrze, a teraz lecę xd narazie

31 sty 23:43

Marcin: Siema i dzięki! emotka

31 sty 23:44

Marcin: Wie ktoś jak się wziąć za to 3?

31 sty 23:48

Saizou: tw. cosinusow

31 sty 23:50

Eta:

a		3		a		2
	=		lub		=
b		2		b		3

31 sty 23:57

Piotr 10: Masz odpowiedź do tego Saizou emotka

31 sty 23:58

Piotr 10: Mi wyszło tak

a		3		a		2
	=		lub		=
b		2		b		3

31 sty 23:59

Eta:

1 lut 00:01

Piotr 10: o super

1 lut 00:02

Marcin: Możecie to rozpisać? emotka

1 lut 00:03

Piotr 10: Ok ja rozpiszę, jak ja to zrobiłem

1 lut 00:03

Marcin: Dzięki! emotka

1 lut 00:04

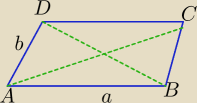
Piotr 10: rysunek

IDBi=f IACI=e e > f

	e²
Wiemy, że		=U{19]{7}
	f²

Z tw. kosinusów Δ ADB

	1
f²+a²+b² −2ab*		=a²+b²−ab
	2

Z tw. kosinusów Δ ACB e²=a²+b² −2ab*cos120⁰=a²+b²+ab

a²+b²+ab		19
	=
a²+b²−ab		7

19a²+19b²−19ab=7a²+7b²+7ab po redukcji mam 6a²−13ab+6b²=0 Δ_a=169b²−144b²=25b² √Δ_a=5b

	13b+5b		3		2
a=		=		b v a=		b
	12		2		3

1 lut 00:07

Piotr 10: Marcin mi to już starczy na dzisiaj

1 lut 00:08

Marcin:

	π		π
f(x)=cos²x+cos²(		+x)−cosxcos(		+x)
	3		3

Powiedzcie mi czy tworzę nową matmę, czy mogę to tak zapisać.

	π		π
f(x)=cosx(cosx+cos(		+x)−cos(		+x))
	3		3

1 lut 00:12

Marcin: Piotr skoro wystarczy to ok, ale i tak wieelkie dzięki za pomoc! emotka

1 lut 00:13

Eta: e −− krótsza przekątna i α= 60^o A ja tak emotka

w każdym równoległoboku : (*) f²+e²= 2a²+2b² i e²=a²+b²−ab

	19		19
z treści zad : f²=		e² =		(a²+b²−ab)
	7		7

	26		7
to (* )		(a²+b²−ab)= 2a²+2b² / *
	7		b²

	a²		a		a²
26		+26−26		= 14		+14
	b²		b		b²

a
	= t >0
b

	a		3		a		2
6t²−13t+6=0 t=		=		v t=		=
	b		2		b		3

1 lut 00:17

Eta: To co napisałeś , to....... bzdura, tak nie można ! Wskazówka

	π		1		√3
cos(		+x) =		*cosx−		*sinx
	3		2		2

1 lut 00:20

Marcin: Dlatego zapytałem o tworzenie nowej matmy. Wiem ze mogę skorzystać z cos(α+β), dzięki Eta emotka

1 lut 00:27

zawodus: Dwa boki równoległoboku zawierają się się w prostych x−y+1=0 i 3x+2y−12=0. Punkt S=(6,4) jest środkiem symetrii równoległoboku. Oblicz jego pole.

1 lut 08:51

Marcin: Pani Milu. Nie potrafię tutaj rysować, ale chciałbym jakoś rozpocząć to zadanie.. Na razie mam tylko tyle..

	a²√3
3ah=
	2

Mnie więcej wiem gdzie ma być ten kąt, ale nie wiem w jakim trójkącie prostokątnym go znaleźć

1 lut 18:04

Piotr 10: Chodzi Ci o zadanie z wczoraj 22:29 ?

1 lut 18:06

Marcin: taak

1 lut 18:13

Piotr 10: Tutaj masz podany gdzie znajduje się ten kąt https://matematykaszkolna.pl/strona/2592.html

1 lut 18:15

Marcin:

	a²√3
Czyli z tego 3ah=		wyliczam h, później wyliczam przekątną sciany bocznej z
	2

pitagorasa i mam wszystko do wyliczenia kąta? Dobry schemat? emotka

1 lut 18:23

Mila:

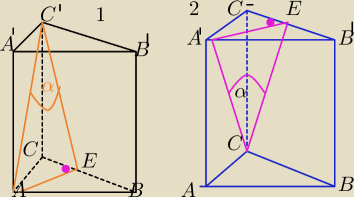
Zgadza się.(Do Marcina) wybierz ten rysunek na którym lepiej "widzisz". Możesz poszukać jak zaznaczyła ten kąt Eta. Ustawiła graniastosłup jak namiot.

1 lut 20:45

Marcin: Liczyłem, liczyłem ii jakieś dziwne liczby mi powychodziły, ale zapytam emotka

	2√13
Czy wynikiem jest		?
	13

1 lut 21:21

Mila: Zgadza się co do joty.

1 lut 21:37

Marcin: Ale mi się humor poprawił, dziękuję emotka

1 lut 21:39

Mila:

1 lut 21:54

Marcin: Gdyby miała Pani jeszcze jakieś zadania, to chętnie spróbuje je rozwiązać, ale nie wiem czy zrobię to dzisiaj emotka

1 lut 21:58

Saizou : dokończ to z trygonometrii i zrób wielomian xd

1 lut 21:59

Marcin: To też, wiadomo emotka

1 lut 22:00

Mila: 1) Ostrosłup prawidłowy czworokątny.

	2
W ostrosłupie prawidłowym czworokątnym wysokość stanowi		długości krawędzi podstawy.
	3

pole powierzchni całkowitej ostrosłupa jest równe 96 cm². Oblicz objętość ostrosłupa.

1 lut 22:07

Marcin:

	2
h=		a
	3

2Pp+4Pb=96

	2
2a²+4(		a*a)=96
	3

	8
2a²+		a²=96 /*3
	3

6a²+8a²=288 14a²=288

	288
a²=
	14

	√288
a=
	√14

Będzie ok?

1 lut 22:22

Mila: Dlaczego masz 2 podstawy?

1 lut 22:30

Marcin: aj. Liczyłem jakby dla graniastosłupa

. Już się poprawiam.

1 lut 22:32

Marcin:

	2
a²+		a²=h²
	3

13
	a²=h²
9

	a√13
h=
	3

	a√13		1
96=a²+(a*		*		)
	3		2

	a²√12
96=a²+		*3
	6

	a²√12
96=a²+		/*2
	2

192=a²+a²√12 192=a²(1+√12)

1 lut 22:46

Marcin: Tak ma to wyglądać? emotka

1 lut 23:12

Mila: NIE. a=6

1 lut 23:32

Marcin: Ma Pani rację. Już nawet wiem gdzie popełniłem błąd.

	1
Powinienem podstawić do tw. pitagorasa		a², a nie samo a², wtedy faktycznie a=6
	2

Przepraszam emotka

1 lut 23:45

Marcin:

1		2
	a²+		a²=h²
2		3

1		4
	a²+		a²=h²
4		9

25
	a²=h²
36

	5
h=		a
	6

Pc=Pp+Pb

	1		5
96=a²+(		a*		a*4)
	2		6

	20
96=a²+		a² /*12
	12

1152=12a²+20a² 1152=32a² 36=a² a=6

	2
H=		a = 4
	3

	1
V=		Pp*H
	3

	1
V=		364
	3

V=48 Mam nadzieję, że teraz jest ok.

1 lut 23:52

Marcin: (x+1)(x+2)(x+3)(x+4)+1 Zapisałem to później tak: (x+1)(x+4)(x+2)(x+3)+1 (x²+5x+4)(x²+5x+6)+1 (x²+5x+4)(x²+5x+4+2)+1 Później jakby wymnażam te nawiasy i mam: (x²+5x+4)(x²+5x+4)+2(x²+5x+4)+1 (x²+5x+4)²+2(x²+5x+4)+1 Jakieś dalsze propozycje Saizou?

2 lut 01:14

Eta: a²+2ab+b²= ....

2 lut 01:29

Eta: widzisz ten wzór? emotka

2 lut 01:30

Marcin: aaaa czyli będzie. (x²+5x+4+1)²? Możemy przyjąć za x²+5x+4 np t? emotka

2 lut 01:31

Marcin: Widzę, ale dopiero po sugestii. Nie wydawał mi się tutaj jakiś oczywisty emotka

2 lut 01:32

Eta: No i po bólu ... wyrażenie jest kwadratem trójmianu

2 lut 01:33

Marcin: No i świetnie emotka

2 lut 01:34

Eta:

2 lut 01:35

Eta: Zostało jeszcze zad 4 emotka

2 lut 01:36

Marcin: Pytanie: Jak mam traktować cos²(x+y)? cosxcosy −sinxsiny? czy może cos²xcos²y−sin²xsin²y

2 lut 01:38

Eta:

cos²(x+y)= [cos(x+y)]²

2 lut 01:40

Marcin: Czyli w moim przypadku wyjdzie:

1		√3		3
	cos²x−		cosxsinx+		sin²x?
4		2		2

2 lut 01:43

Piotr 10: Zad 4. 31 sty 22:29

	π		π
f(x)=cos²x+cos²(		+x) − cosx*cos(		+x)
	3		3

	π		π		π		√3
cos²(		+x)=[cos		*cosx − sin		*sinx]²=0,25cos²x −		cosxsinx +
	3		3		3		2

0,75 sin²x

	π		√3
cosx*cos(		+x)=0,5cos²x −		cosxsinx
	3		2

	√3		√3
f(x)=cos²x+0,25cos²x −		cosxsinx +0,75 sin²x − 0,5cos²x +		cosxsinx =
	2		2

3		3		3		3
	cos²x+		sin²x=		( sin²x+cos²x)=
4		4		4		4

c.n.w

2 lut 10:23

Saizou : emotka

2 lut 10:26

Marcin: Dzięki. emotka

Rozumiem jak robić takie zadanie, ale często mylę się w obliczeniach, co mnie straaasznie irytuje

2 lut 10:27

Saizou : to jeszcze wielomian został xd

2 lut 10:28

Piotr 10: Który ?

2 lut 10:28

Marcin: Z pomocą Ety wielomian został już ogarnięty (patrz kilka postów wyżej emotka

2 lut 10:29

Piotr 10:

2 lut 10:30

Saizou : faktycznie, nie widziałem go w tej ilości postów

2 lut 10:30

Marcin: Nie szkodzi

Skończyły mi się zadania emotka

2 lut 10:32

Piotr 10: Jak chcesz to mogę dać Ci jedno jakieś

2 lut 10:32

Marcin: Pewnie. Z waszą pomocą zawsze jakoś ogarnę

2 lut 10:33

Piotr 10: Zadanie Dany jest wielomian W(x)=x⁸ −4x⁴+3. a) oblicz sumę i iloczyn pierwiastków tego wielomianu b) rozwiąż nierówność W(x) ≤ 0 Ja lecę, Saizou na pewno Ci pomoże w razie problemów emotka

2 lut 10:35

Marcin: Dzięki emotka

2 lut 10:36

5-latek: Marcin zobacz tu godz 16:28 https://matematykaszkolna.pl/forum/234904.html

2 lut 10:40

Saizou : zad. 6 Ile wszystkich dzielników naturalnych ma liczba 792? zad 7 Znajdź wszystkie pary liczb całkowitych, których suma jest równa ich iloczynowi? zad 8 udowodni, że jeżeli dodatnie liczby a,b,c tworzą w tej kolejności ciąg geometryczny oraz a≠1,

	1		1		1
b≠1, c≠1, to liczby		,		,		dla każdego x∊(0:+∞)\{1} tworzą w
	log_ax		log_bx		log_cx

tej kolejności ciąg arytmetyczny zad 9

	1		1		1
Udowodnij, że suma		n³+		n²+		n jest liczbą naturalną dla każdej liczby
	6		2		3

naturalnej n

2 lut 10:40

Marcin: Saizou zauważyłem, że dajesz bardzo dużo zadań typu 'udowodnij' emotka

5−latek: Nie chcę już wkurzać bezendu tym, że mu się wbijam w jego zadania emotka

2 lut 10:42

Saizou : zadania na dowodzenie są bardzo przyjemne

(PS. pokaż jak zapisujesz przebieg dowodu

)

2 lut 10:43

Marcin: Pytanie co do tego wielomianu od Piotra: Mogę sobie podstawić za x⁴ jakąś zmienną?

2 lut 10:44

Saizou : możesz wszystko, tylko aby było to zgodne z prawami matematyki xd

2 lut 10:45

5-latek: Mozesz je rozwiazac tutaj

2 lut 10:47

Marcin: t²−4t+3 Δ=4 √Δ=2 x₁=1 x₂=3 Chyba tak nie będzie emotka

2 lut 10:49

Saizou : no i dalej emotka

2 lut 10:51

Saizou : tylko że nie x₁ i x₂ a t₁ i t₂ emotka

2 lut 10:51

Marcin: Co do Twojego zadania Saizou.. 792:2=396 396:2=198 198:2=99 99:3=33 33:3=11 11:11=1 2³*3²*11=792 Teraz wszystkie możliwe iloczyny tych liczb to dzielniki, ale jest ich troche emotka

2 lut 10:52

Saizou : nie ma ich znowu aż tak dużo

ale najpierw dokończ zadanie Piotra

2 lut 10:53

Marcin: Czyli w takim razie x₁=1, a x₂=81?

2 lut 10:54

Saizou : no nie bo masz podstawienie t=x⁴ x⁴=1 lub x⁴=3, zatem.....

2 lut 10:55

Marcin: x₁=1 x₂=⁴√3?

2 lut 10:57

Saizou : coś mało tych rozwiązań emotka

2 lut 10:57

Marcin: Jeszcze na minusie ma się rozumieć?

2 lut 10:58

Saizou : tak

2 lut 11:00

Marcin: Czuje się jak na korkach normalnie, fajnie emotka

Przepraszam za takie podstawowe błędy, ale to może przez to, że nie spałem całą noc :x

2 lut 11:00

5-latek: Marcin udalo CI sie . Ale nastepnym razem zrob zalozenie co do t bo masz wielomian stopnia parzystego czyli t=x⁴ dla t≥0

2 lut 11:00

Marcin: 5−latek czyli gdyby jakieś miejsce zerowe wyszło <0, to od razu odpada z rozwiązania?

2 lut 11:02

Saizou : 5−latek nie trzeba pisać tego założenia tylko trzeźwo myśleć bo np. x⁴=−3 no to wiadomo że sprzeczność xd

2 lut 11:03

5-latek: Tak gdyby jakies t wyszlo ujemne to to rozwiazanie odpada gdyz nie istnieje pierwiastek stopnia parzystego z liczby ujemnej Natomiast ze stopnia nieparzystego tak

2 lut 11:04

Saizou : ja to wiem, ale mówię że nie trzeba pisać tego założenia, choć dla świętego spokoju lepiej napisać xd

2 lut 11:05

5-latek: Ja wiem ze TY wiesz. ja to pisalem do Marcina emotka

2 lut 11:06

Marcin: ok. Co do drugiego zadania od piotra. x∊<−⁴√3;−1> ∪ <1;⁴√3>

2 lut 11:06

Saizou : spoko no to teraz niech Marcin skończy zadanko

2 lut 11:07

Saizou : emotka

a teraz pierwsza część zadania

2 lut 11:09

Marcin: Suma to wiadomo = 0 A iloczyn: To będzie 1*(−1)*3¹^/⁴*(−3¹^/⁴) =9¹^/⁴

2 lut 11:11

Saizou :

no i gites

2 lut 11:12

Marcin: Jedziemy dalej. xy=x+y xy−x=y x(y−1)=y

	y
x=
	y−1

Tu doszedłem

2 lut 11:18

Saizou : i dalej

2 lut 11:20

zawodus: dzielników jest 4*3*2=24

2 lut 11:21

Saizou : choć ja proponuje inne rozwiązania x+y=xy (x−1)(y−1)=1

2 lut 11:23

Saizou : zawodus masz rację

2 lut 11:23

5-latek: Marcin jak sie uporasz z tym zadniem to masz nastepne log_x(x²+3x−3)>1 rozwiaz ta nierownosc . ja juz musze isc do rodzicow dlatego dalem je teraz emotka

2 lut 11:24

Saizou : ja też muszę lecieć, jak by co to wrzuć rozwiązania na pewno ktoś sprawdzi

2 lut 11:25

Marcin: to muszą być liczby całkowite czyli jakbyśmy dali coś większego niż 2 za y, to będziemy mieli ułamek. Z drugiej strony nie możemy dać za y nic mniejszego od 0, bo też będzie ułamek. Czyli y= albo 0, albo 2, bo 1 daje nam zero z mianowniku. Czyli podstawiając.. 0=x 2x=x+2 x=2 x=0 y=0 lub x=2 y=2?

2 lut 11:25

Marcin: zawodus 24 to dośc dużo

2 lut 11:26

Marcin: 2 korepetytorów mnie zostawia emotka

Miłego dnia życzę emotka

2 lut 11:27

zawodus: Marcin, a wiesz jak to policzyć?

2 lut 11:29

zawodus: te dzielniki?

2 lut 11:30

Marcin: wszystkie możliwe iloczyny liczb 2,2,2,3,3,11. Chyba że znasz szybszy sposób, to słucham emotka

2 lut 11:31

zawodus: Twoim sposobem nie policzysz liczby dzielników liczby: 2¹⁰*4⁵*12¹⁰

2 lut 11:33

zawodus: wsk. powiąż to z kombinatoryką emotka

Wracamy do przykładu liczby 2³*3²*11

2 lut 11:34

Artur: czy ktoś mógłby mi stąd pomóc z następującym zadaniem: na podstawie definicji monotoniczności wyznacz monotoniczność następującej funkcji:

x

x+5

prosiłbym o dokładne rozwiązanie i wyjaśnienie, nie było mnie w szkole ze względu na chorobę, a w podręczniku same "suche" fakty bez przykładów. Chciałbym, żeby ktoś rozwiązał mi ten przykład, żebym mógł wzorując się na nim, zrobić resztę. Wiem tyle, że funkcja jest rosnąca przedziałami, ale nie potrafię tego zrobić z definicji. Z góry bardzo dziękuję

2 lut 11:36

Marcin: No jak nie? 2*2 2*2*2 2*2*2*2*3*3*11 2*2*3 2*11 3*11 2*2*2*11 2*2*3*11 . .. . W sumie będzie 24 takie kombinacje.

2 lut 11:36

Marcin: będą* emotka

2 lut 11:36

zawodus: A co z liczbą 2¹⁰*4⁵*12¹⁰

Ile mamy tutaj dzielników naturalnych?

2 lut 11:37

zawodus: Artur najpierw poszukaj w książce def. monotoniczności... Najlepiej byłoby gdybyś założył nowy temat, bo tutaj rozmawiamy na inne tematy

2 lut 11:38

Marcin: Tutaj jest już inna sprawa, bo tej liczby nie rozbijałem. Mój sposób dlatego właśnie jest zły, bo nie da się nim wyliczyć dzielników dużych liczb.

2 lut 11:39

Marcin: Artur jeżeli chcesz tylko sam wynik, to podstaw kilka liczb za x i sprawdz czy funkcja rośnie czy maleje emotka

2 lut 11:40

Artur: no wiem, ale jak zobaczyłem jakie zadania rozwiązujecie, to stwierdziłem, że takie to dla Was będzie na 5min.

2 lut 11:41

Artur: Wiem, że funkcja rośnie, nie zależy mi na samym wyniku, tylko na tym jak do tego wyniku dojść na podstawie definicji. Z książki dowiedziałem się, że x1<x2; f(x1)−f(x2)<0

	5		5
wyszło mi, że 1 −		− 1+		<0
	x1+5		x2+5

	5		5
−		+		<0
	x1+5		x2+5

2 lut 11:43

zawodus: Marcin twój przykład: 2³*3²*11 Teraz liczymy: liczba 2 może się pojawić w naszym dzielniku 0 razy, 1 raz lub 2 razy lub 3 razy −−− 4 możliwości liczba 3 może się pojawić w naszym dzielniku 0 razy, 1 raz lub 2 −−− 3 możliwości liczba 11 może się pojawić w naszym dzielniku 0 razy, 1 raz −−− 2 możliwości Teraz znana zasada mnożenia i mamy: 4*3*2=24 emotka

Teraz twoje zadanie to moja liczba emotka

2¹⁰*4⁵*12¹⁰ policz ile ma dzielników.

2 lut 11:45

zawodus: Artur mamy tam pewną implikację.

2 lut 11:46

Marcin: ok. Będzie 11*6*11 emotka

2 lut 11:47

Artur: czyli, że to x2>x1? kurczę, to chyba nie dla mnie

2 lut 11:48

zawodus: to właśnie tutaj był ukryty haczyk emotka

ta reguła o której piszę działa jeśli rozłożymy liczbę na czynniki pierwsze

jeszcze raz emotka

2 lut 11:48

zawodus: funkcja rosnąca: x₁<x₂ ⇒ f(x₁)<f(x₂) malejąca na "odwrót"

2 lut 11:49

Marcin: Fajna sprawa. Dzięki za fajną wskazówkę. Przyda się nie raz emotka

2 lut 11:50

zawodus: wynik ile będzie?

2 lut 11:52

Artur: to wiem, ale nie potrafię zinterpretować tego, co dostałem

2 lut 11:53

Marcin: Przecież napisałem. 11*6*11 emotka

2 lut 11:53

Mila: 23:52 Dobrze.

2 lut 11:55

zawodus: Marcin, źle, bo 4 nie jest pierwsza, ani liczba 12 też nie jest pierwsza.

2 lut 11:57

Marcin: log_x(x²+3x−3)>1 zał: x>0 x²+3x−3>0 x²+3x−3>x Dobrze myślę? Teraz wszystko liczę i mam przedział.

2 lut 11:58

Marcin: Można to tak rozbić? 2¹⁰*(2²)⁵*3¹¹*(2²)¹¹

2 lut 12:02

zawodus: a podstawa może być 1

Nierówność rozwiązujesz w przedziałach x∊(0,1) oraz x∊(1, +∞)

2 lut 12:03

zawodus: Marcin można to przecież działania na potęgach. Teraz pomnóż je i zapisz w postaci potęg liczb pierwszych. Potem możesz stosować ten zabieg, który ci podałem wyżej.

2 lut 12:04

Marcin: zawodus, ale moje założenia będą poprawne o ile później wyrzucę z dziedziny 1?

2 lut 12:05

Marcin: 2¹⁰*2¹⁰*3¹¹*2²² =2⁴²*3¹¹ Czyli teraz będzie 43*12, powiedz że taaak emotka

2 lut 12:09

zawodus: Tak tylko musisz to robić w dwóch przedziałach. Zmienia ci się znak nierówności w każdym z przedziałów.

2 lut 12:10

zawodus: Zadanie z dzielnikami jest ok.

tylko zmieniłeś mój przykład trochę

2 lut 12:12

Marcin: x2+3x−3>x dla x(1;+∞) x2+3x−3<x dla x(0;1) tak?

2 lut 12:14

zawodus: tak.

2 lut 12:31

Marcin: Zad 8. Zapisałem sobie a=a b=aq c=aq²

1		1		2
	+		=
log_a_q		log_a_q²		log_a_q

Jak ja nie lubię logarytmów emotka

2 lut 16:08

Saizou : napisz cały dowód emotka

2 lut 19:16

Piotr 10: Saizou dobrze przepisane jest zadanie numer 9 ''2 luty 10:40'' ?

2 lut 19:44

Marcin: Saizou chętnie bym go napisał, ale nie trawię logarytmów i nie wiem jak się za to zabrać

2 lut 19:46

Saizou : dobrze jest

jak chcesz możesz je rozwiązać emotka

2 lut 19:47

Piotr 10: 9 zrobię, a reszty to mi się nie chce

2 lut 19:47

Saizou : to może Piotr się skusi, a dowód banalny emotka

2 lut 19:48

Marcin: Co do 9.. można pomnożyć przed 6 i wyciągnąć n przed nawias i dalej kombinowac?

2 lut 19:51

Marcin: w 8 dowód jest banalny?

2 lut 19:52

Saizou : zał: b²=ab

	2		1		1
teza:		=		+
	log_bx		log_ax		log_cx

Dowód log_xb²=log_xac→2log_xb=log_xa+log_xc zmieniając podstawę logarytmu otrzymamy

2		1		1
	=		+		ckd
log_bx		log_ax		log_cx

2 lut 19:53

Saizou : to zrób 9 w pełnym zapisie

2 lut 19:54

Eta:

	n
9/ L=		*(n+1)(n+2)
	6

2 lut 19:54

Marcin: Dla mnie nie był banalny emotka

myślisz że coś tego typu może pojawić się na maturze?

2 lut 19:55

Saizou : i Eta popsuła zabawę

2 lut 19:56

Eta:

2 lut 19:56

Saizou : to zadanie było żywcem z arkuszy maturalnych od nowej ery z R

2 lut 19:56

Saizou : Eta a masz jakieś ciekawe zadanka ?

2 lut 19:57

Marcin: Eta, Saizou. Wy już jesteście po maturze? emotka

chciałbym mieć waszą wiedzę emotka

2 lut 19:58

Piotr 10: Pisać rozwiązanie do 9 ?

2 lut 19:58

Saizou : jak tam chcesz Piotrze Twoja wola emotka

ja do matury jeszcze trochę mam (do maja) a Eta jeśli dobrze pamiętam to I LO

2 lut 19:59

Marcin: Napisz, napisz.

2 lut 20:00

Eta: zad1/ Wykaż jeżeli liczba x jest całkowita nieparzysta, to liczba: x⁶−x⁴−x²+1 jest podzielna przez 32

2 lut 20:00

Piotr 10: Ja 9 widzę tak

1		1		1		n³+3n⁺2n		n(n²+3n+2		n(n+1)(n+2)
	n³+		n²+		n=		=		=
6		2		3		6		6		6

n(n+1)(n+2) − to iloczyn trzech kolejnych liczb naturalnych, z których na pewno jedna dzieli się przez 2 a druga dzieli się przez 3, a więc 2*3=6 A więc suma jest liczbą naturalną dla każdej n∊N

2 lut 20:01

Marcin: To powiem wam, że wróżę wam dobrze zdaną maturę i jestem w szoku że aż tak ogarniacie emotka

2 lut 20:03

Eta: zad2/ Wykaż ,że suma kwadratów trzech kolejnych liczb całkowitych, z których najmniejsza jest postaci 2n−3 ,n∊C z dzielenia przez 3 daje resztę 2

2 lut 20:04

Saizou : a tak na prawdę Eta to nauczycielka a ja skromny tegoroczny maturzysta emotka

2 lut 20:05

Eta:

2 lut 20:05

Saizou : Eta to ja założę nowy wątek do tego emotka

2 lut 20:05

Eta: ok emotka

2 lut 20:07

Marcin: Wbije popatrzeć na wasze rozwiązania, emotka

Skoro nauczycielka, to nie wiem teraz jak mam się zwracać emotka

2 lut 20:07