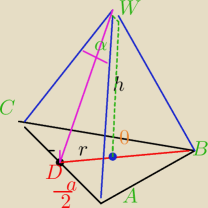
ostroslup 5-latek: zadanie dla Piotra 10 W ostroslupie prawidlowym trojkatnym dana jest wysokosc h i kat plaski przy wierzcholku ostroslupa alfa . Znalezc objetosc graniastoslupa majacego z danym ostroslupem wspolna podstawe i rowna wysokosc Mysle ze odczytasz rysunek .

Piotr 10: Później postaram się to zrobić .

5-latek: Dobrze . A powiedz czy jest ciekawe ?

Piotr 10: Nie robiłem jeszcze takiego typu zadania, wydaję się na pierwszy rzut oka ciekawe

Piotr 10: Mam dane tylko wysokość i kąt alfa ? Krawędzi podstawy i promienia nie mam danego, tak?

5-latek: tak

Piotr 10: ten kąt alfa jest zawarty między dwoma sąsiednimi krawędziami bocznymi ?

5-latek: tak . Tak jak na rysunku

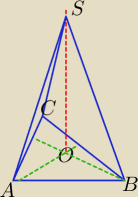Piotr 10: I∠ASBI=α ISOI=h ; Niech IASI=b i IABI=a ΔASB z tw kosunów a²=2b²−2b²*cosα

	a
b=
	√2−2cosα

ΔASO

	2		a√3
IAOI=		*
	3		2

IASI²=IAOI²+ISOI²

	3a2
b2=		+h2
	9

a2		3a2
	=		+h2
2−2cosα		9

	3(2−2cosα)
a=h*√
	1+2cosα

V_{graniastosłupa}=P_p*h

	3h2(2−2cosα) * √3
Pp=
	4*(1+2cosα)

	3h2(2−2cosα) * √3		3√3h3(2−2cosα)
V=		* h =
	4*(1+2cosα)		4*(1+2cosα)

Piotr 10: 5−latek sprawdź jak możesz : ) . W końcowy wyniku jeszcze można skrócić przez 2

Ajtek: Cześć 5−latek . Ale rysunek Tok myślenia jest okej. Rachunków nie sprawdzałem.

5-latek: Witam Ajtek Przepraszam z eteraz dopiero sie witam ale mialem pilny telefon i musialem wyjechac . Piotr ja to zadanie rozwiazalem tak

	a2√3
Pp=
	4

W trojkacie prostokatnym WOD h²=WD²−OD²

	a		x
W trojkacie AWD WD=		ctg
	2		2

	a√3
OD=		bo to promiren kola wpisanego w podstawe
	6

a2

x

a2

a2

x

1

to h2=

ctg2

−

=

(ctg2

−

4

2

12

4

2

3

	4h2
to a2=
	x   1   ctg2 −   2   3

	x		1
Podstawilen a2 do wzoru na Pp dostalem PP= U{h2√3}{ctg2		−
	2		3

	h3√3
Wiec V=Pp*h to V=
	x   1   ctg2 −   2   3

	x		1
Jeszce mi kolega mowil zeby ctg2		−		przeksztalcic na iloczyn (ale tego nie wiem
	2		3

jak ) i mam dostac taki wynik

	x   h3√3sin2   2
V=
	x   x   4sin(60+ sin(60−   2   2

alfa zapisalem jako x bo mi sie lepiej pisalo MOze wiesz TY albo moze Ajtek jeszce spojrzy jka to przeksztalcic na ten iloczyn

5-latek:

Ajtek:

	x
sin2		=1−cosx
	2

Ajtek: Mianownik wygląda tak:

	x		x
4*sin(60o+		)*sin(60o−		)
	2		2

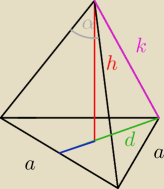Saizou : W ostroslupie prawidlowym trojkatnym dana jest wysokosc h i kat plaski przy wierzcholku ostroslupa alfa . Znalezc objetosc graniastoslupa majacego z danym ostroslupem wspolna podstawe i rowna wysokosc

	2	a√3		a√3
d=			=
	3	2		3

k²=h²+d²

	3a2		1
k2=h2+		=h2+		a2
	9		3

	1
k=√h2+		a2
	3

a²=k²+k²−2k*kcosα a²=2k²−2k²cosα

	1		1
a2=2(h2+		a2)−2cosα(h2+		a2)
	3		3

	2		2
a2=2h2+		a2−2h2cosα−		a2cosα
	3		3

3a²=6h²+2a²−6h²cosα−2a²cosα a²+2a²cosα=6h²−6h²cosα a²(1+2cosα)=6h²(1−2cosα)

	1−2cosα
a2=		*6h2
	1+2cosα

	1−2cosα
Vg=Pp*h=		*6h3
	1+2cosα

5-latek: Jeszce raz witam tak wyglada mianownik

Ajtek: Siema, siema . Skoro Saizou rozwalił zadanie, to mi się nie chce gimnastykować . Czesc Saizou .

Saizou : Cześć Ajtek musiałem uciec z forum, a raczej uciec przed sprzątaniem

Ajtek: Cwaniaczek .

Saizou :

5-latek: Saizou spojrz tez na te zadania https://matematykaszkolna.pl/forum/234914.html .