funkcja kwadratowa

funkcja kwadratowa majsk: Rownanie x²+6x+c²=0 ma dwa rozne rozwiazania wtedy i tylko wtedy, gdy? proszę bardzo o pomoc! emotka

1 lut 00:14

Marcin: Δ>0 emotka

1 lut 00:14

majsk: a jak obliczyć c? emotka

1 lut 00:26

majsk: ?

1 lut 00:28

Marcin: 6²−4c²>0 emotka

1 lut 00:30

majsk: aaa, dziękuję! emotka

a mogłbyś spojrzeć na to zadanko https://matematykaszkolna.pl/forum/234812.html

1 lut 00:33

majsk: skoro rozwiąząłam i mam, że c=3 v c=−3 co dalej?

1 lut 00:36

Marcin: Masz przedział, a nie dwa rozwiązania emotka

1 lut 00:36

majsk: jaki przedział? bo troszkę się pogubiłam, jeżeli mialbyś cierpliwość i wytłumaczył byłoby miło emotka

1 lut 00:39

majsk: juz wiem, juz wiem, juz wiem!

dziekie!

1 lut 00:40

majsk: wyjdzie c∊(−∞,−3) u (3,∞) ?

1 lut 00:42

Marcin: A już miałem próbować tłumaczyć emotka

1 lut 00:43

Marcin: 36−4c²>0 36>4c² 9>c² Ma być mniejsze od 9, czyli jak jest przedział? emotka

1 lut 00:45

majsk: co za błąd, oczywiscie że c∊(−3, 3) , ale ze mnie niezdara!

dziękuję bardzo! emotka

1 lut 00:46

Marcin: emotka

1 lut 00:47

majsk: masz chwilę, zeby wyjaśnić mi jeszcze kilka zadanek? emotka

1 lut 00:49

Marcin: Pisz. Postaram się jak mogę emotka

1 lut 00:53

majsk: 1. Funkcja kwadratowa f(x)=9x²−12x+4 może przyjąć dla pewnego argumentu wartość równą A. −10 B. −6 C. −4 D. 0 2. Dwie funkcje f(x) i g(x) przecinają się w punktach (−4,3) oraz (−1,0) Równanie f(c)=g(x) ma dwa rozwiązania, których suma jest równa... ?

1 lut 00:58

Marcin: A wartości są na X czy Y? emotka

1 lut 01:04

Ajtek: Zad. 1. znajdź współrzędne wierzchołka.

1 lut 01:04

majsk: wartość to y emotka

1 lut 01:07

majsk: p=2/3 q=0 tak?

1 lut 01:08

Ajtek: yhy emotka

1 lut 01:08

Marcin: Tak, czyli jaka jest odpowiedź?

1 lut 01:09

Ajtek: Bardziej q było istotne emotka

1 lut 01:09

majsk: czyli tak jakby q=y_w zatem ta wartość to 0 ?

1 lut 01:09

Ajtek: yhy emotka

1 lut 01:10

Marcin: Tak, a teraz istotny jest współczynnik przy x², dlaczego? emotka

1 lut 01:10

majsk: ma to związek z tym, że jest dodatni, zgadza się? (trochę się bawię w podchody, ale nie chcę strzelić gafy, wybaczcie) emotka

1 lut 01:13

Ajtek: Znalazłeś y_w, a jak ramionka paraboli są skierowane (góra, dół)

1 lut 01:14

Marcin: Wtedy parabola skierowana jest 'do góry' (współczynnik większy od 0) i zbiór wartości jest wtedy równy (q;+∞)

1 lut 01:15

majsk: góra

1 lut 01:15

majsk: dziękuję, jesteście wielcy i bardzo cierpliwi!

a drugie zadanko? emotka

1 lut 01:16

Marcin: myślę, myślę, ale treść tego zadania jest dla mnie jakaś niezrozumiała, wybacz

1 lut 01:24

majsk: a z takim rysunkiem (mniej wiecej) kropki to pkt przecięcia

1 lut 01:33

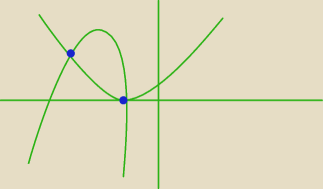
majsk: rysunek

1 lut 01:36

Marcin: To byłem w stanie sobie wyobrazić, ale nie chce Cię wprowadzać w błąd jakimś złym rozwiązaniem. emotka

1 lut 01:39

majsk: znam odpowiedź suma będzie = −5

1 lut 01:41

majsk: ale i tak dziekuje bardzo! spisałeś sie na medal! emotka

1 lut 01:42

ZKS: Zbiór wartości funkcji kwadratowej dla współczynnika dodatniego przy najwyższej potędze to ZW_f = [q ; ∞). f(x) = 9x² − 12x + 4 f(x) = (3x − 2)²

1 lut 01:52

ZKS: Zadanie 2. Skoro wiemy że funkcje f(x) oraz g(x) przecinają się dwóch miejscach o współrzędnych (−4 ; 3) oraz (−1 ; 0) to rozwiązaniem równania f(x) = g(x) są x₁ = −4 oraz x₂ = −1. Zatem suma tych rozwiązań to x₁ + x₂ = −4 + (−1) = −5.

1 lut 01:55

Marcin: Ja chciałem iść w tym kierunku, że rozwiązaniami są 3 i 0 (bo w końcu X to argument), ale dobrze zrobiłem, że nie pisałem odpowiedzi emotka

1 lut 01:57

ZKS: 3 oraz 0 to są rzędne (wartości funkcji) natomiast −4 oraz −1 to odcięte (argumenty).

1 lut 02:03

Marcin: Ok, ok. Dzięki za wytłumaczenie emotka

1 lut 02:05

ZKS: Na zdrowie. emotka

1 lut 02:07