Rozwiaz rowannie Mikolaj: Rozwiąż równanie sin(x+ π 6)cosx +sin x cos(x− π 6)= 1/2 x∊<0,2π >

zawodus: Sin(α+β)=sinαcosβ+sinβcosα

Marcin: Napisz do jakoś bardziej czytelnie.

Mikolaj: oj moj blad tam jest Rozwiąż równanie sin(x+ π/6)cosx +sin x cos(x+ π/6)=0,5

PrzyjacielMikołaja: https://matematykaszkolna.pl/forum/75806.html SZUKAĆ SIĘ NAUCZ

Mikolaj: wyszlo mi ze sinx=0 dobrze?

Mariush: ktos mi sprawdzi? x= 0 lub x = π

Mariush: zamiast zera x = ^π₂

Mikolaj: rozpiszesz mi bo nie wiem skad Ci sie to wzielo?

mario: jestem beznadziejny z matmy

Mariush: nie jestem pewny,czy dobrze zrobilem)

Mariush: Mario,z rysunkow tez

Marcin: Może mi ktoś powiedzieć co robię źle?

	1
sin(x+30)cosx+sinxcos(x−30)=
	2

	√3		1		√3		1		1
(		sinx+		cosx)cosx + sinx(		cosx+		sinx)=
	2		2		2		2		2

√3		1		√3		1		1
	sinxcosx+		cos2x+		sinxcosx+		sin2x=		/*2
2		2		2		2		2

√3sinxcosx+cos²x+√3sinxcosx+sin²=1 √3sinxcosx+√3sinxcosx=0 2√3sinxcosx=0 sinxcosx=0 2sinxcosx=0 sin2x=0

mario: A CO POWIESZ NA TO ?

Marcin: Uczyć się matmy Panowie, a nie rysować snake'a, czy "CHWDP"

Mikolaj: chyba sie nie doczekam prawidlowego rozwiazania

PrzyjacielMikołaja: JESTEŚMY Z TOBĄ MIKOŁAJ TRZYMAJ SIĘ !

mario:

Marcin: Mógłby ktoś sprawdzić dlaczego mam źle? został tu ktoś jeszcze?

Mariush: mi tez tak wyszlo

Marcin: Tyle że to nie jest dobrze Przynajmniej tutaj jest inaczej: https://matematykaszkolna.pl/forum/75806.html

Mariush: Marcin,stad x = ^π₂ lub x = π ?

Mariush: tam inny przyklad

mario:

Marcin:

	π
Dlaczego		i π?
	2

Mikolaj: mi wyszlo x=0 , x=π , x=2π

Marcin: Szedłbym w tym kierunku co Mikołaj Popatrz na sinusoide

Mariush: tez tak bym szedl

Marcin: wredulus pospolitus gdybyś mógł sprawdzić moje rozwiązanie na górze, to byłym bardzo wdzięczny.

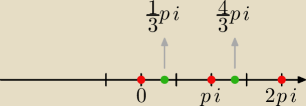
Bogdan: To od początku.

	π		π		1
sin(x +		) cosx + sinx cos(x +		) =
	6		6		2

	π		π
sin(x +		+ x) = sin
	6		6

	π		π		π		π
2x +		=		+ k*2π lub 2x +		= π −		+ k*2π
	6		6		6		6

	2
2x = k*2π lub 2x =		π + k*2π
	3

	1
x = k*π lub x =		π + k*π
	3

	1		4
x∊{0,		π, π,		π, 2π}
	3		3

Marcin: Czyli jedno rozwiązanie mieliśmy dobrze, a drugie nam jakoś uciekło? Mógłby Pan sprawdzić gdzie popełniam błąd w liczeniu?

ZKS: Marcin Ty liczyłeś

	π		π		1
sin(x +		)cos(x) + sin(x)cos(x −		) =
	6		6		2

natomiast Bogdan

	π		π		1
sin(x +		)cos(x) + sin(x)cos(x +		) =
	6		6		2

Marcin: dość dużo to zmienia Ale dalej nie wiem jak z moim wynikiem w sumie jest. Nie ma mi kto tego sprawdzić.

Bogdan: Rachunki Marcinie masz poprawne, ale sposób nieco zawiły i gubiący niektóre rozwiązania. W równaniach trygonometrycznych czasami przy niektórych ścieżkach rozwiązania nie pokazują się wszystkie rozwiązania. Trzeba np. unikać parzystych potęg. Dobranoc

Bogdan: bo w poprawionej wersji jest plus

Marcin:

	√3
Licząc ten drugi przykład takim samym sposobem wychodzi mi coś dziwnego, bo sin2x=
	3

Dziękuję za odpwiedz

ZKS: Tylko że cos²(x) − sin²(x) ≠ 1.

ZKS: A zapewne Ty tak sobie przyjąłeś że to jest to samo co cos²(x) + sin²(x) = 1.

Marcin:

	2√3
Inną głupotę strzeliłem, ale spróbowałem się poprawić. Wyszło ze sin2x=		, co też
	3

jest jakimś dziwnym wynikiem

ZKS:

√3		1		√3		1		1
	sin(x)cos(x) +		cos2(x) +		sin(x)cos(x) −		sin2(x) =
2		2		2		2		2

	1		1
√3sin(x)cos(x) +		[cos2(x) − sin2(x)] =
	2		2

√3		1		1
	sin(2x) +		cos(2x) =
2		2		2

	π		1
sin(2x +		) =
	6		2

Wychodzi to samo co napisał Bogdan w jednej linijce.

Marcin: Ja próbowałem podstawiać za cos²x ⇔ (1−sin²x), nie można tak?

^Bartek^: a to co?

ZKS: I co Ci to da jak tak zamienisz?

Marcin: Nie wiem. Próbuję jak mogę, a że nie mam doświadczenia w tego typu zadaniach, to wychodzi to co wychodzi. Dzięki wielkie za pomoc ZKS

ZKS: Jeżeli dopiero zaczynasz to kiedyś nabierzesz doświadczenia jakim sposobem najlepiej zrobić zadanie o ile będziesz rozwiązywać dużo przykładów. Nie ma za co. Z zamianą cos²(x) = 1 − sin²(x)

	1		1		1		1
√3sin(x)cos(x) +		−		sin2x(x) −		sin2(x) =
	2		2		2		2

√3sin(x)cos(x) − sin²(x) = 0 sin(x)[√3cos(x) − sin(x)] = 0. I rozwiązujesz dalej.

Marcin: Dokładnie do tego momentu doszedłem. W pierwszym wyniku źle po prostu podstawiłem. sinx=0 √3cosx−sinx=0?

Marcin:

	π
2cos(x+		) = 0 ma być niby coś takiego, ale skąd to się w ogóle wzięło?
	6

ZKS: Znasz wzory na sin(x − y) albo cos(x + y)?

Marcin: No jakby nie było, to od nich zaczynałem liczenie tych przykładów

ZKS:

	π
To powinieneś wiedzieć jak z √3cos(x) − sin(x) = 0 zrobić cos(x +		) = 0.
	6

Marcin: w sumie masz rację. Jak tak teraz patrzę, to wiem skąd to się bierze

ZKS: Właśnie to samo zrobił Bogdan na samym początku z równaniem zauważ to.

Marcin: No to zwinięcie do sin(x+y) u Pana Bogdana widzę, ale z takim zwinięciem i tak miałbym problem, ale to można wyćwiczyć

ZKS: Jeżeli porobisz podobne przykłady to później od razu będziesz zauważał te wzory.

Marcin: Gdzie mógłby znaleźć podobne przykłady?

ZKS: W zbiorach byś musiał poszukać.

Marcin: W sumie to już jest w moje kwestii czy sobie znajdę czy nie Dziękuję za poświęcony czas o 4 nad ranem

ZKS: Jeżeli byś chciał to bym mógł poszukać jakieś zadania takiego typu. Jak coś napisz kiedy będziesz chciał to poszukam czegoś. Nie ma za co siedzę bo się uczę.

Marcin: Ja jestem zawsze gotowy na nowe zadania

ZKS: Napisz post dzisiaj to poszukam na wieczór.

Marcin: Napiszę z takim ogólnym pytaniem, może ktoś jeszcze mi coś powrzuca

ZKS: O to mi chodzi. Na pewno sporo osób coś Ci ciekawego da.

Marcin: ok. To jeszcze raz wielkie dzięki i do dzisiaj

ZKS: Na zdrowie.