policzyć ekstremum, wklęsłości, wypukłości
d4mian: 4x3+2x2+1
policzyć ekstremum, wklęsłości, wypukłości..
29 sty 13:24
wredulus_pospolitus:
no i w czym problem

29 sty 13:25
Patronus:
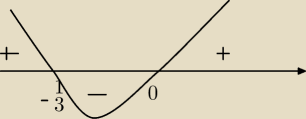
f'(x) = 12x
2 + 4x
f'(x) = 0 ⇔ 12x
2 + 4x = 0
4x(3x+1) = 0
miniumum w punkcie 0
| | 1 | |
f rośnie dla x∊(−∞;− |
| )∪(0;∞) |
| | 3 | |
f''(x) = 24x
f''(x) = 0 ⇔ 24x = 0
x = 0
punkt przegięcia x = 0
f wklęsła dla x<0
f wypukła dla x>0
29 sty 13:30
d4mian: | | 1 | |
okej, dzięki wielkie... zastanawia ,mnie tylko czemu maximum jest − |
| skoro jest na |
| | 3 | |
minusie a 0 jest wyżej i brane za minimum
29 sty 13:45
ICSP: To w końcu w x = 0 jest minimum czy punkt przegięcia ?

29 sty 13:51
wredulus_pospolitus:
d4mian ... bo to są minima i maksimum LOKALNE

(czyli największa/najmniejsza wartość w jakimś
tam kawałku funkcji) ... a Twoje pytanie świadczy, że dopiero zaczynasz siadać do materiału, a
na zajęciach nie uważałeś (nie wspominając już o nauce na bieżąco)
29 sty 14:02
d4mian: @wreduluspospolitus: nie ważne co świadczy a co nie... pytam i poszukuje odpowiedzi bo ja
patrząc na wykres zastanawia mnie czemu max jest na wartości ujemnej a minimum na nieujemnej,
albo umiesz wytłumaczyć albo sie nie udzielaj
29 sty 14:12
wredulus_pospolitus:
d4mian ... odpowiedź ode mnie uzyskałeś ... jeżeli nie potrafisz jej 'wyłowić' to się nie pytaj
(tonacja odpowiednia do twojej)
29 sty 14:17
d4mian: ale od czego to zależy, po lewej zawsze będzie maximum a po prawej minimum?
29 sty 14:28
29 sty 14:30
d4mian: (
https://matematykaszkolna.pl/forum/209281.html )
" funkcja ma maksimum gdy wykres pierwszej pochodnej zmienia znak z + na −
− funkcja ma minimum gdy wykres pierwszej pochodnej zmienia znak z − na + "
@ ICSP : i to jest odpowiedź na temat! thx
29 sty 14:39
Patronus:
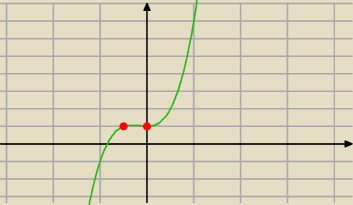
i widzisz max lokalne (takie siodło) jest po lewej stronie osi Y
a minumum lokalne dokładnie w 0
jak widać nie są to najmniejsze lub największe wartości funkcji w dziedzinie, tylko w jakimś
małym otoczeniu

29 sty 14:43

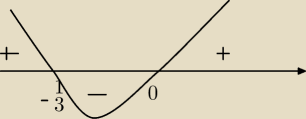 f'(x) = 12x2 + 4x
f'(x) = 0 ⇔ 12x2 + 4x = 0
4x(3x+1) = 0
f'(x) = 12x2 + 4x
f'(x) = 0 ⇔ 12x2 + 4x = 0
4x(3x+1) = 0

 (czyli największa/najmniejsza wartość w jakimś
tam kawałku funkcji) ... a Twoje pytanie świadczy, że dopiero zaczynasz siadać do materiału, a
na zajęciach nie uważałeś (nie wspominając już o nauce na bieżąco)
(czyli największa/najmniejsza wartość w jakimś
tam kawałku funkcji) ... a Twoje pytanie świadczy, że dopiero zaczynasz siadać do materiału, a
na zajęciach nie uważałeś (nie wspominając już o nauce na bieżąco)
 i widzisz max lokalne (takie siodło) jest po lewej stronie osi Y
a minumum lokalne dokładnie w 0
jak widać nie są to najmniejsze lub największe wartości funkcji w dziedzinie, tylko w jakimś
małym otoczeniu
i widzisz max lokalne (takie siodło) jest po lewej stronie osi Y
a minumum lokalne dokładnie w 0
jak widać nie są to najmniejsze lub największe wartości funkcji w dziedzinie, tylko w jakimś
małym otoczeniu 