Geometria Blue: Punkty A, B są punktami przecięcia prostej y=3/5x−6 z osiami układu współrzędnych. Oblicz pole równoległoboku ABCD, którego wierzchołek D ma współrzędne (1,4) Chcę tylko znać wynik, bo wyszło mi 94, a nie mam odpowiedzi. Ktoś policzy i powie, czy tak samo mu wyszło?

sushi_ gg6397228: szukasz jeleni ? zapisz swoje rozwiazanie, to sie sprawdzi czy nie ma błędów rachunkowych

Blue: jakich jeleni? Tylko pytam, bo nie chcę tutaj dwóch stron obliczeń zapisywać

5-latek: https://matematykaszkolna.pl/forum/233764.html

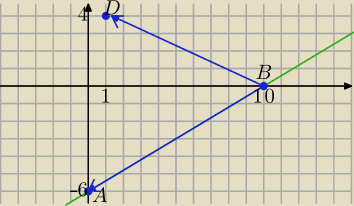
Eta: A(0,−6) , B(10,0) → → BA=[−10, −6] ,BD= [−9, 4] , → → P= |d(BA, BD)|= | −10*4−(−6)*(−9)|= |−76|= 76 [j²]

Eta: @Blue Jak widzisz ....... mnie zajęło to dwie linijki

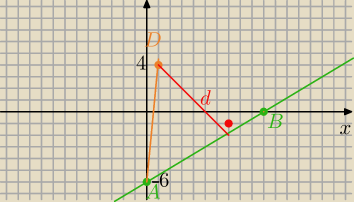
Mila: D=(1,4) (3/5)x−6=0 /*5 3x=30 x=10 m. zerowe B(10,0) A(0,−6) |AB|=√(10²+6²=√136

	3
y=		x−6 postac kierunkowa
	5

3x−5y−30=0 postac ogólna równania prostej AB Odległość D od AB

	|3*1−5*4−30|
d=
	√32+52

	47
d=
	√34

	47
P▱=√136*		=2*47=94
	√34

II sposób AB^→=[10,6] AD^→=[1,10] P=det|10 6| 1 10| P=10*10−6=94

Eta: Mila czemu mnie wyszło P= 76 ?

sushi_ gg6397228: 40+54=.... dokończ

Mila: 9*6=54

Eta: O kurde dzięki