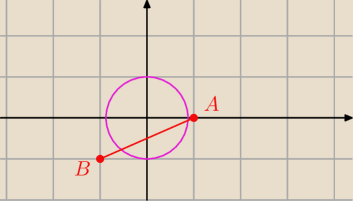
Geometria Analityczna Radek: 1. Dane są punkty A (1,0),B(− 1,1) . Punkt C należy do okręgu o równaniu x²+y²=1 . Znajdź współrzędne punktu C , tak aby pole trójkąta było największe. Oblicz to pole. Jak teraz odszukać ten punkt C ? Proszę o wskazówkę

Mila: Podpowiedź. Np. Napisz równanie prostej prostopadłej do AB (zawierającej wysokość Δ) przechodzącej przez środek okręgu.

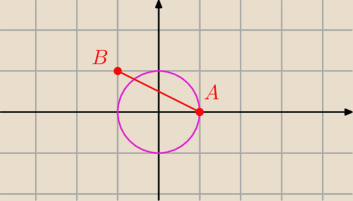
Radek: A=(1,0) B=(−1,1)

	1−0		1
aAB=		=−
	−1−1		2

y=2x+b S=(0,0) y=2x

Eta: Teraz rozwiąż układ równań tej prostej z okręgiem

Mila: Punkt B jest w innym miejscu

	−1
a=
	2

Teraz masz znaleźć punkt wspólny y=2x i x²+y²=1

Radek: A jeszcze mam pytanie ? Czemu ta wysokość musi przechodzić przez środek okręgu ?

Radek:

Mila: Najdłuższa cięciwa to średnica, zrób sobie rysunek poglądowy i doświadczalnie się przekonaj ( nie jest to dowód, ale łatwiej Ci bedzie zrozumiec)

Radek: Dobrze.

Radek: A jeśli by było najmniejsze pole ?

Eta: Najmniejsze pole = 0

Radek: Pole nie może być równe 0 ?

Eta: No właśnie , więc nie może być pytania o najmniejsze pole

Radek: Czyli wysokość przy największym polu musi przechodzić przez środek okręgu ?

Radek: Już zrozumiałem.

Mila: To pięknie.

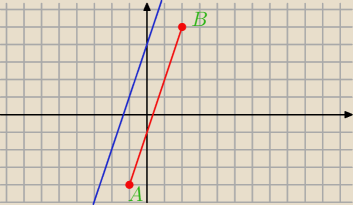
Radek: 2. Wierzchołek C trójkąta ABC leży na prostej y = 3x + 4 , a pozostałe wierzchołki mają współrzędne A = (− 1,− 4) i B = (2,5 ) . Uzasadnij, że pole trójkąta ABC nie zależy od wyboru punktu C i oblicz to pole Te proste są równoległe ale co dalej ? C=(x,3x+4)

5-latek: czym bedzie tu wysokosc ?

5-latek: Albo inaczej . Czym jest odleglosc kazdego punktu na prostej y=3x+4 od prostej AB?

Eta:

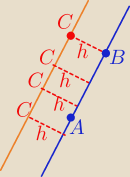
	1
P=		|AB|*h , h−−− odległość między prostymi równoległymi jest ....
	2

Radek: Zrozumiałem.

Eta:

Radek: 3/ Dany jest okrąg o równaniu x²+y²−2x+6y+5 = 0 . Napisz równania stycznych do danego okręgu, prostopadłych do prostej o równaniu x−2y=0 (x−1)²−1+(y+3)²−9+5=0 (x−1)²+(y+3)²=5 S=(1,−3) r=√5 x−2y=0 −2y=−x 2y=x

	1
y=		x
	2

y=−2x+b I ?

Radek: ?

Eta: 1 sposób podstaw do równania okręgu y= −2x+b otrzymasz równanie z parametrem "b" i nałóż warunek na deltę : Δ=0 otrzymasz "b" 2 sposób odległość "d" środka S od stycznej : d= r powodzenia

Radek: x²−(−2x+b)²−2x+6(−2x+b)+5=0 x²−(4x²−4bx+b²)−2x−12x+6b+5=0 x²−4x+4xb−b²−14x+6b+5=0 x²−b²−18x+4xb+6b+5=0 x²−(18+4b)x−b²+6b+5=0 i teraz Δ=0 ?

Eta: tak (tylko ..... nie sprawdzałam twoich rachunków

Eta: 2 sposób jest łatwiejszy ( spróbuj rozwiązać i tym sposobem

Radek: Drugim sposobem również wyszło

Eta: No to ,który sposób jest łatwiejszy? jak myślisz?

bezendu: Każdy sposób jest dobry.

Radek: Drugi

Eta: Ejjj bezendu Ciebie nie pytałam

bezendu: Ej Eta zajrzy tutaj https://matematykaszkolna.pl/forum/233250.html.

bezendu: https://matematykaszkolna.pl/forum/233250.html

Eta: Poza tym pytałam,który łatwiejszy a nie, który "dobry" ? a może kwaśny ?

bezendu: pig.. ?

Radek: Dziękuję za pomoc.

Eta: @bezendu Dla Radka

Radek: 4. Wyznacz równanie takiej prostej przechodzącej przez punkt A (− 4,6) , która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2. Podpowiedź

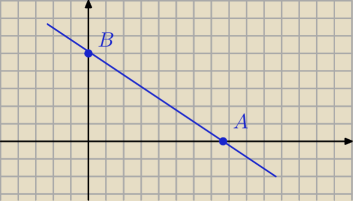
Ada: A=(x,0), B=(0,y) Jaki jest wzór na pole tego trójkąta

Radek:

	1
P=		ah
	2

Ada: nie, z wykorzystaniem współrzędnych punktów A i B (tych moich, nie twojego A )

Radek: Ale skąd wiadomo, że B będzie takie ?

Ada: Jeżeli punkt B leży na osi y, to jego współrzędna x musi być zerem, to samo się tyczy punktu A(znów mojego, nie fortunie go nazwałam), jeżeli A leży na osi x to y musi być zerem.

Ada: Chodzi mi o pole trójkąta prostokątnego ABO, gdzie O=(0,0)

Radek: Chodzi Ci o pole trójkąta o podanych wierzchołkach taki wzór jak w tablicy ?

Ada: Nie, nie ten wzór z wektorami. Zauważ, że to jest trójkąt prostokątny, a jak się ma w takim trójkącie pole tego trójkąta do długości przyprostokątnych

Radek: Jedna przyprostokątna jest wysokością

Ada: a druga podstawą. Teraz jakie są ich długości

Radek: długość podstawy 8

	1
P=		*|BO|*8
	2

P=2 4|B0|=2

	1
|BO|=
	2

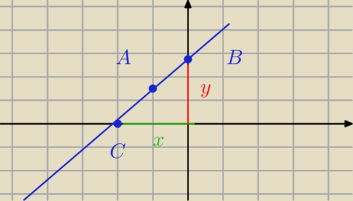
Ada: Dlaczego długość podstawy 8 Przecież parę razy podkreślałam, że popełniłam kolizję oznaczeń i A na moim rysunku nie jest twoim A. Może teraz: C=(x, 0), B=(0,y) A=(−4,6)

	1
P=		xy (*)
	2

Musisz teraz za pomocą A wyliczyć równanie prostej (zostanie ci 1 literka nie określona). Podstawiasz to równanie do wzoru na pole (*) i wyliczasz tę brakującą literkę.

Radek: y=−x+2 takie równanie wyszło ?

Ada: Nie. 6=−4a+b ⇒ b=6+4a Czyli prosta ma wzór k: y=ax+6+4a Dla C=(x,0) :

	6+4a
0=ax+6+4a ⇒ x=
	−a

Dla B=(0,y) y=6+4a

	1		6+4a
(*) P=		*		*(6+4a)=2 −> rozwiązać, wychodzą 2 rozwiązania.
	2		−a

Radek: Dzięki, już wyszło.