Wielomiany Maslanek: Wielomiany Dowieść, że jeżeli równanie x³+px+q=0 ma trzy różne rozwiązania to p<0. :(

bezendu: Wzory Viet'a dla 3 stopnia.

Maslanek: Próbowałem rozpisać (x−a)(x−b)(x−c) i porównać. To sprowadza się przecież do tego samego

bezendu: Musi wyjść ! x₁x₂x₃=−q x₁+x₂+x₃=0 x₁x₂+x₁x₃+x₂x₃=p (x₁+x₂+x₃)²=..

Maslanek: No tak . Korzystając z tego ostatniego już sympatycznie wychodzi 2p=−(a²+b²+c²), gdzie a≠b≠c. Rzeczywiście Dzięki, dzięki

bezendu: No to gitara

Eta:

PW: Myślałem dzisiaj nad tym zadaniem, ale nie działał mi internet, więc dopiero teraz. Zależało mi na dowodzie "szkolnym", chyba większość licealistów nie zna wzorów Viete'a dla wielomianu wyższego stopnia niż 2 . Wśród trzech różnych liczb istnieją dwie, których iloczyn jest nieujemny. Niech te pierwiastki wielomianu mają oznaczenia a i b. a³ + p•a + q = 0 b³ + p•b + q = 0. Po odjęciu stronami a³ − b³ + p(a−b) = 0 (a−b)(a²+ab+b²) + p(a−b) = 0. Z założenia a i b są różnymi liczbami, można więc podzielić stronami przez (a−b): a²+ab+b² + p = 0 (1) a²+ab+b² = −p Wzięliśmy takie a i b, że ab≥0, a więc lewa strona (1) jest dodatnia, co oznacza, że p < 0.

Maslanek: Bardzo mi się podoba

PW: , praca nie poszła na marne.

Eta: Achhh ... jaka radocha

PW: Eta, uszanowanie. Ty też pewnie siedzisz tu dla tej biblijnej radochy (ziarno trafiło na podatny grunt, jak mówi Pismo. Nie mówi? To może jakoś tak ...

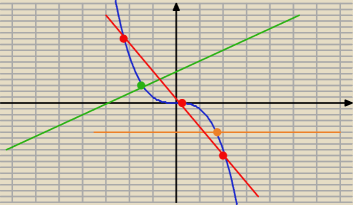
Bogdan: Taki ilustracyjny sposób (nie dowód) x³ + px + q = 0 ⇒ px + q = −x³ y = −x³ (funkcja potęgowa) (niebieska linia) y = px + q (linia prosta): dla p>0 (zielona linia) jest jedno rozwiązanie, dla p = 0 (pomarańczowa linia) też jest jedno rozwiązanie, dla p<0 (czerwona linia) są trzy rozwiązania

PW: O, takiego nauczyciela powinien mieć każdy. Czy Ty też postawiłbyś czwórkę uczniowi, który podał takie rozwiązanie? Istota rzeczy się liczy, formalizmy dopiero później.

Bogdan: Gdyby było polecenie: "pokaż, że ... " to przyjąłbym takie rozwiązanie, ale w przypadku polecenia: "udowodnij, że ... " oczekiwałbym oprócz rysunku dodatkowego uzasadnienia.