Obliczyć ekstrema i zbadać monotoniczność funkcji : f(x)=ln(x^2)+x Fernanda: Bardzo proszę o pomoc , obliczyłam zadanie do połowy i mi nie wychodzi ... może ktoś wie co źle robie , ale pomoże mi rozwiązać Obliczyć ekstrema i zbadać monotoniczność funkcji : f(x)=ln(x²)+x na początku wyznaczyłam dziedzine x>o potem pochodną y'=2/x+1 przyrównuje do zera 2/x+1=0 mnoże razy x i wychodzi x=−2 chyba zrobiłam coś źle pomocyy

Bizon: ...a dlaczego dziedzina x>0 .... a może tylko x≠0

Fernanda: Chodzi o rozwiązanie całego zadania..ponieważ ja średnio sobie z tym radzę. Dziedzina x>0 ponieważ argumenty logarytmu naturalnego musza byc wieksze od 0

Ajtek: Liczbą logarytmowaną jest x², zatem x²>0 ⇒x>0 lub x<0 ⇒ x∊R\{0} Witaj Bizon.

Bizon: witaj Ajtek −

Bizon: ..dobrze sobie radzisz ... dawaj dalej Policzyłaś warunek konieczny ...sprawdzaj drugi ... pewnie wyjdzie Ci maximum ... a potem bierz się za otoczenie ZERA i za monotoniczność −

Fernanda: tylko , ze nie wiem właśnie jak wyliczyć drugi :(:( mam tylko jeden a powinna wyjsc parabola?

Bizon: jaka parabola − Mówię a warunkach istnienia ekstremum. Jaki jest drugi warunek ?

Fernanda: nie wiem ?

fernanda: prosze , czy moglbys mi pomoc to obliczyć?

Bizon: można tak .... https://matematykaszkolna.pl/strona/387.html a można drugą pochodną

fernanda: no wiem , ale mam tylko jedno miejsce przeciecia z osia x jak wyznaczyć drugie?

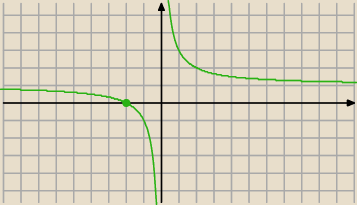
Bizon: jest tylko jedno miejsce zerowania się pochodnej ... pytam o drugi warunek Tyle, że Ty nie czytasz Pochodna "zeruje się" dla x=−2 ... czyli w tym punkcie może być ekstremum Sprawdzamy drugi warunek ... zmianę znaku pochodnej przy przejściu przez ten punkt. Wykres pochodnej masz na rysunku Zauważ, że pochodna zmienia znak z + na − ...czyli ?

Fernanda: maleje?

Bizon: https://matematykaszkolna.pl/strona/387.html