Proszę o wyjaśnienie imię: Dana jest funkcja określona wzorem f(x)=(x−5)2+m zbiorem wartosci tej funkcji jest przedział od (7;+∞) oznacza to że

imię: m=−5 m=5 m=7 m=−7

Bizon: oczywiście miało być f(x)=(x−5)²+m ... poczytaj o postaci kanonicznej − https://matematykaszkolna.pl/strona/69.html

imię: Tak. Jakoś nie rozumiem. Obliczam deltę, współrzędne p i q i źle mi wychodzi

Bizon: ... a po co Ci Δ skoro masz gotową postać kanoniczną −

imię: A co mi po tej postaci kanonicznej

Bizon: rosiłem poczytaj ... dałem linka ... Odpowiedz sobie co we wzorze funkcji f(x)=(x−5)²+m wyjaśnia 5 a co m.

imię: p=5 q=m

imię: O to chodzi

5-latek: Zbior wartoscci funkcji oddczytujemy na jakiej osi . Osi Ox ? czy osi OY ?

imię: Z osi y

5-latek: Nie z y tylko OY . Ale OK czyli do wyznaczenia zbioru wartosci funkcji bedzie mam potrzebma wspolrzena y_w=q tej funkcji napisales/as ze w naszym wzorze funkcji q=m mamy wyznaczyc ile to m sie rowna . jest tak jesli wspolczynnik a<0 to Z_wf nalezy (− oo q> jesli a >0 to zbior wartosci funkcji kwadratowej Z_wf nalezy <q,oo) zapamietaj to sobie i popatrz teraz swoje zadanie i napisz ile wynosi m

imię: No i trzeba było tak od razu. 7 to prawidłowa odpowiedź

imię: Dzięki

Bizon: a potrafisz teraz naszkicować wykres tej funkcji?

5-latek: Imie to co ja napisalem Tobie to sa wiadomosci z lekcji . Te wiadomosci napewno przekazal nauczyciel . To samo probowal CI przekazac Bizon Tylko chcial zebys sam /a do togo doszedk/la . naszkicuj tutaj teraz wykres tej funkcji

imię: Parabola ma ramiona w górę bo a jest dodatnie. Potem wystarczy obliczyc delte i zobaczyć co wyjdzie Chyba

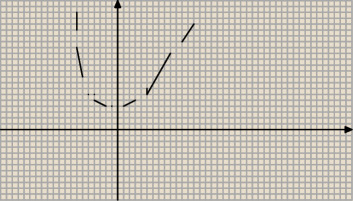
5-latek: No widzisz . jednak nie rozumiesz ideii postaci kanonicznej Postac kanoniczna pozwala na odczytanie od razu wierzchokla paraboli Zauwaz ze nie ma potrzeby w tym przypadku liczenia delty(bo nie bedzie miejsc zerowych x₁ i x₂) . Masz wspolrzedne wierzcholka x_w=p=5 i y_w=q=7 . zatem ten wierzcholek bedzie lezal nad osia OX ( czyli wykres tej funkcji nie bedzie przecila osi OX ) Rysunek jaki jest taki jest ale pokazuje o co chodzi