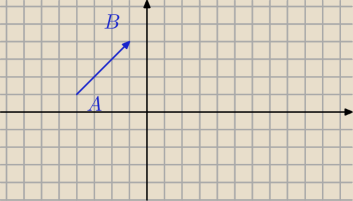
wektor bezendu: Jeśli mam taki wektor to jego współrzędne to AB=[3,3] ? Jak policzyć jego długość

jakubs: https://matematykaszkolna.pl/strona/1624.html

bezendu: Dzięki

bezendu: A jakieś inki do nauki i zadań w wykorzystaniem wektorów ?

jakubs: Całą potrzebną teorię znajdziesz tutaj. Zadania brałem tylko ze zbiorów, więc żadnych ciekawych stron nie mam.

bezendu: dobra ale ja nie wiem jak te wektory wykorzystać.

jakubs: do zadań z geometrii analitycznej ?

bezendu: Właśnie robię analityczna ale unikam wektorów. Daj jakieś zadania z tej analitycznej gdzie trzeba wykorzystać wektor ?

jakubs: np. Oblicz obwód trójkąta ABC: a) A(2,2), B(6,−6), C(6,5)

jakubs: np. zadanie nr 10 https://matematykaszkolna.pl/strona/3606.html

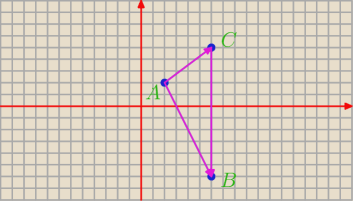
bezendu: AB=[4,8] AB=4√5 AC=[4,3] AC=5 CB=[0,11] CB=11 Obw=16+4√5 Obw=4(4+√5

bezendu: Jakub ? A to 10 to jak z wektora ?

jakubs: Dobrze Czy trójkąt ABC jest równoramienny? Czy jest on prostokątny ? a) A(−4,2), B(0,−1), C(6,7)

jakubs: W 10 trzeba wykorzystać odległość dwóch punktów od siebie : https://matematykaszkolna.pl/strona/1248.html Zadanko nie typowo z wektorów, więc tak średnio z nim trafiłem, ale wydaje mi się ciekawe.

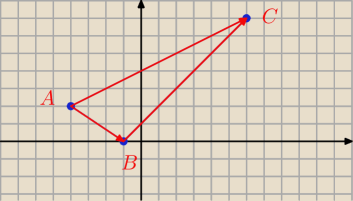
bezendu: AC=[10,5] AC=5√5 AB=[3,−2] AB=√13 BC=[7,7] BC=7√2 Trójkąt ABC jest prostokątny

bezendu: Ja umiem zrobić to zadanie 10 bez problemu, ale wektorami mam ciężko.

bezendu: Chyba to 10 jednak prościej normalnie bez wektorów zrobić

jakubs: "ale wektorami mam ciężko" czegoś nie rozumiesz ? Z wektorów to musisz znać wzorki i podstawiać cała reszta zależy od zadanka i czego dokładnie potrzebujesz.

bezendu: Ok, dzięki poszukam za zadania info czegoś z wektorami

jakubs: Jeśli chcesz to jutro mogę Ci podesłać jakieś zadanka ze zbiorów które posiadam. Jakieś tam mam Nowa Era, Pazdro, Kiełbasa i parę innych coś tam może znajdziesz z wektorów

bezendu: Mam kiełbasę ale komuś pożyczyłem i jeszcze jej nie odzyskałem. Będę wdzięczny za każde zadanie z wektorów.

5-latek: AC²=BC²+AB² (5√5)²=(p{13)²+(7√2)² 125 nie rowna sie 13+98 wiec trojkat nie jest prostokatny

jakubs: A(−4,2), B(0,−1) AB=[3,−2] Powinno być AB=[0−(−4),−1−2] AB=[4,−3] B(0,−1), C(6,7) BC=[7,7] Powinno być BC=[6−0,7−(−1)] BC=[6,8] Trójkąt jest prostokątny.

Lorak: Np. takie zadanie: Dane są 3 wierzchołki równoległoboku A=(−4,−1), B=(1,2), D=(−2,4). Wyznacz współrzędne czwartego wierzchołka równoległoboku, oblicz jego obwód i pole. Jeśli będziesz potrzebował to wrzucę jutro rozwiązanie.

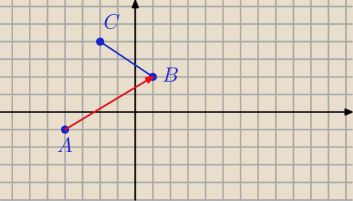
bezendu: długość wektora AB jest równa długośći wektora CD i przyrównać współrzędne ?

bezendu: Lorak jutro ? zobacz godzinę

5-latek: Wskazowka do zadania Loraka Rowne wektory maja na plaszczyznie XOY rowna wspolrzedne

bezendu: 5−latek czyli to co napisałem ?

bezendu: AB=[5,3] AB=√34 i dalej się zaciąłem ?

Eta: → → AD=BC AD=[2,5] , BC=[x_C−1, y_C−2] ⇒ x_C−1=2 i y_C−2=5 ⇒ C(3,7) AB=[5,3] |AB|=√5²+3²=..... |AD|=√2²+5²=... P(ABCD)= | d(AB, AD)|= |2*3−5*5|= ..... Ob=......

Lorak: AB→ = [5,3] AB→ = DC→ C=[x_c,y_c] DC→ = [x_c−x_d , y_c−y_d] DC→ = [x_c+2, y_c−4] [5,3] = [x_c+2, y_c−4] x_c+2=5 y_c−4=3 x_c=3 y_c=7 C=(3,7)

bezendu: Dzięki Eta

Eta: Przy wektorach "strzałki" ( nie chciało mi się pisać

bezendu: Tak wiem, Dziś jeszcze porobię zadania z tych wektorów.

Eta:

5-latek: Wczoraj CI nie odpowiedzialem gdyz sie nagle zle poczulem i musialem odejsc od komputera Musisz zaczac od prostych zadan dotyczacych obliczania dlugosci i wspolrzednych wektora typu 1Znajdz wspolrzedne konca B wektora AB [−2,5] jeezeli jego poczatek znajduje sie w punkcie A(−1,5) 2. Dane sa 3 wektory a=[1,0] b=[0,2] c=[1,−1] znajdz dlugosc wektora x=2a−b+3c bedzie tu tez mnozenie wektora przez liczbe zadanie nr 3 Dany jest jeden z wierzcholkow trojkata A(2 −5) i wektrory bokow AB[4,1] i BC[3,−2] Znajdz pozostale wierzcholki i wektor CA I na koniec zadanko nr4 Dane sa trzy punkty A(2,−1) B(1,3) i C(−1,1) ktore sa wierzcholkami trojkata . Znalezc katy tego trojkata . Tylko masz skorzystac nie z twierdzenia cosinusow ale z wlasnosci iloczynu skalarnego . Masz policzyc z iloczynu slalarnego wszystkie 3 katy be z kombinowania ze 3 to 180−(alfa + beta )