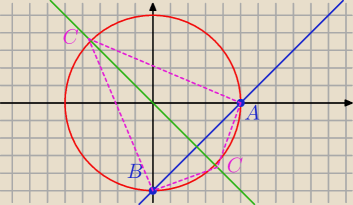
geo RS: Ostrokątny trójkąt równoramienny ABC o podstawie AB jest wpisany w okrąg o równaniu x²+y²=25 . Punkty A i B leżą na prostej o równaniu y=x−5 oblicz współrzędne a,b,c x²+(x−5)²=25 x²+x²−10x+25−25=0 2x²−10x=0 2x(x−5)=0 x=0 lub x=5 y=−5 lub y=0 wyznaczyłem środek odcinka AB=(2,5;−2,5) współczynnik kierunkowy a_AB=−1 równanie proste prostopadłej do prostej ab i przechodzącej przez środek odcinka Ab y=−x Teraz przecięcie się prostej y=−x z okręgiem ? x²+x²=25 2x²=25 x²=12,5

	5√2		5√2
x1=		x2=−
	2		2

	5√2		5√2
y1=−		y2=
	2		2

OK ?

Godzio: Ok

Maslanek: Wygląda dość mądrze

RS: Godzio http://www.zadania.info/d36/922836 a u nich tylko jeden punkt ?

Godzio: Ano tak, nie popatrzyłem na informację o "ostrokątności". Musisz sprawdzić warunek: c² < a² + b²

RS: https://matematykaszkolna.pl/forum/230649.html Eta spójrz proszę

RS: Godzio ale skąd wiadomo, że on ma być ostrokątny ? Nie podano nic w poleceniu ?

Eta: W poleceniu masz " ostrokątny trójkąt.........

Godzio: "Ostrokątny trójkąt równoramienny ...." Podano

Eta: Zapomniał przeczytać początku zadania?

RS: Godzio to jest warunek dla trójkąta ostrokątnego ?

RS: Eta tak

RS: c<a+b nierówność trójkąta ?

Godzio: RS, to co podałem to warunek na to, żeby trójkąt był ostrokątny, c to najdłuższy bok

RS: Dzięki