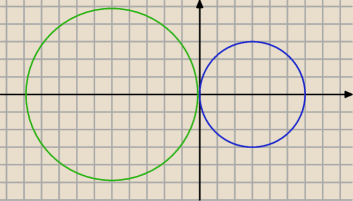
g RS: Znajdź równania prostych stycznych do dwóch okręgów: (x−3)²+y²=9 i (x+5)²+y²= 25 . Wskazówki ?

Marcin: Z podobieństwa trójkątów wylicz sobie punkt leżący na prostej która jest styczna do tych dwóch okręgów. Jej jedną współrzędną już znasz, bo leży na y=0 (x,0)

RS: Hmm ?

Marcin: Powiedz mi jak się tutaj rysuje, to może postaram się to jakoś przedstawić Bo jakoś mi to nie wychodzi

ZKS: Zapisz sobie równanie prostej w postaci ogólnej następnie odległości od tej prostej do środków tych okręgów ma być równa ich promieniom.

RS: Klikasz rysuję i po rozwinięciu masz w drugim rzędzie ikonę z układem równań. klikasz i rozmieszczasz układ, jeśli chcesz okrąg to 4 ikona w pierwszym rzędzie

RS: Zaraz spróbuje coś zrobić

Marcin: Chyba jestem jakiś lewy, bo jak klikam na układ to wychodzi mi całkiem inny niż Twój. Jak go w ogóle przybliżyć? http://screenshu.com/static/uploads/temporary/l7/lq/da/o19ums.jpg

RS: Jak już wybierzesz to odjedź trochę tymi liniami.

Marcin: Spróbujmy inaczej Styczna musi mieć równanie y = ax + b (bo to prosta) Także mamy do rozwiązania układ równań

⎧	y=ax+b
⎨	(x−3)2+y2=9
⎩	(x+5)2+y2= 25

Wylicz z tego a i b i rozwiązanie gotowe

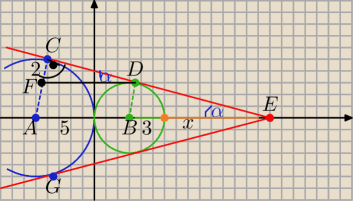
Eta: Z podobieństwa trójkątów AEC i BDC

5		11+x
	=		⇒ x= 9 , zatem E(15,0)
3		x+3

|FD|= |AB|= 8 , |FC|= 5−3=2 to:

	√15
|CD|=√60= 2√15 tgα=
	15

	√15
zatem wsp. kierunkowy stycznej CE : a= −
	15

	√15		√15
czyli styczna AC ma równanie: y= −		(x−xC)= −		x +√15
	15		15

druga styczna EG jest prostą symetryczną do AC względem osi OX

	√15
zatem ma równanie : y=		−√15
	15

i trzecia styczna to oś OY : x=0 Pozdrawiam

Eta: Poprawiam chochlika : z podobieństwa trójkątów AEC i BDE

RS: Dziękuję Eta choć ja nigdy nie chciałem gotowca

Eta: pigor zawsze pisze "gotowce" to i ja raz .... mogę

RS: Tylko do rozwiązań pigora trzeba dorosnąć A Twoje rozumiem

Eta: No i o to chodzi

RS: Eta spójrz proszę https://matematykaszkolna.pl/forum/230649.html