Różniczkowanie Studentka: Zbadaj przebieg funkcji. Proszę tylko o sprawdzenie a) f(x)=3x²+x−12 1) D=R 2) przecina sie z osią y w punkcie P=(0;−12) 3) granica x→∞3x²+x−12=∞ granica x→−∞3x²+x−12=−∞ 4)funkcja nieparzysta bo f(−x)=−f(x) 5)f'(x)=3x²+x−12=6x+1

	1		1
funkcja rośnie dla x>−		a maleje dla x<−
	6		6

nie wiem jak policzyć ekstrema ale mi sie wydaje że ich nie ma... ale nie wiem...

	1
6)Punkt przegięcia to −
	6

7)jak nie ma ekstremów to też nie ma asymptot Robię pierwszy raz to sama wiec nie wiem czy to w ogóle jest dobrze

Ajtek: 387 tutaj masz o ekstremum.

J: Przecież to zwykły trójmian kwadratowy.A więc Δ = ... i miejsca zerowe....itd.

Eta: To jest przecież funkcja kwadratowa, wykresem parabola , ramionami do góry osiąga minimum w wierzchołku , itd........ https://matematykaszkolna.pl/strona/3413.html

Studentka: myslałam ze do ekstremum bierze sie pod uwagę pochodne.... a cze początek jest dobrze pkt 1,2,3,4?

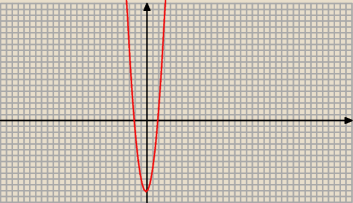
Janek191: To jest zwyczajna funkcja kwadratowa ! f(x) = 3 x² + x − 12 więc 1) Tak 2) Tak 3) Nie 4) Nie 5) Tak − pochodna

	−1		1		1
p =		, więc q = f(p) = f( −		) = −12
	6		6		12

	1
Posiada minimum lokalne dla x = p = −
	6

	1
ymin = −12
	12

6) Nie ma punktu przegięcia

Studentka: Więc jaka będzie granica?

	1		12
granica x→∞3x2+x−12=granica x→∞x2(3+		−		)=∞
	x		x3

	1		12
granica x→−∞3x2+x−12=granica x→−∞ x2(3+		−		)=−∞
	x		x3

Gdzie tu jest błąd?

Eta: x→±∞ g= +∞

Studentka: a jak się liczy parzystość?

wredulus_pospolitus: sprawdzasz: f(x) = f(−x) czyli zamiast 'x' wstawiasz '−x' i sprawdzasz czy 'wyjdzie to samo'

wredulus_pospolitus: czyli: f(x) = 3x²+x−12 to f(−x) = f(x) = 3(−x)²+(−x)−12 = 3x² −x − 12 f(−x) ≠ f(x) <−−−− funkcja nie jest parzysta (co nie znaczy ze jest nieparzysta )

Eta: f(−x)=f(x) −− to funkcja parzysta f(−x)= 3x²−x−12 ≠ 3x²+x−12 −−− funkcja nie jest parzysta

Janek191:

	1		12
3x2 + x − 12 = x2*( 3 +		−		) → +∞ , gdy x → − ∞
	x		x2

	1		12
bo		→ 0 ,		→ 0 , x2 → +∞
	x		x2

Studentka: wzór na: Parzystą f(−x)=f(x) Nieparzysta f(−x)=−f(x) Czyli ta funkcja nie jest ani parzysta ani nieparzysta więc? jak napisac odpowiedz?

Janek191: Wykres funkcji parzystej jest symetryczny względem prostej x = 0 Wykres funkcji nieparzystej jest symetryczny względem punktu ( 0; 0 )

Janek191: Odp. Ta funkcja nie jest parzysta i nie jest nieparzysta.

Studentka: Dziękuje Janek191 Dziękuję Wam wszystkim bo bez Was pewnie bym sobie nie poradziła...

Studentka: Jeszcze kilka pytań czyli ta funkcja jest wypukła bo f''(x)=6 czyli >0 i mam problem z określeniem asymptoty tutaj... bo powinna być ukośna, bynajmniej tak myślę.

Studentka: ?

wredulus_pospolitus: a dlaczego uwazasz ze bedzie ukosna

wredulus_pospolitus:

	f(x)
aby była ukosna to granica lim		by musiała być równa jakieś stalej
	x

	f(x)
a Ty masz w najwyższa potęge w funkcji x2 ... więc granica		to będzie +/−∞
	x

czyli brak ukośnej

wredulus_pospolitus: co do wklesłości/wypukłości masz narysowaną ta funkcję ... ona jest wklesla czy wypukła

Studentka: wypukła