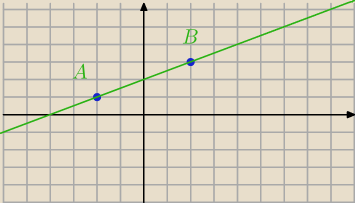
, RS: Na płaszczyźnie dane są punkty A = (2,3) i B = (− 2,1) (patrz rysunek). Zbadaj, czy punkty K = (36,21 ) i L=(−37,−15) leżą po tej samej stronie prostej AB . Podaj odpowiedź i jej uzasadnienie y=0,5x+2 Ale co dalej jak to zbadać ?

Rafał28: Ja bym poprowadził prostą przez punkty K, L i jeżeli punkt wspólny prostej KL oraz prostej AB byłby pomiędzy punktami K, L to leżały by te punkty po przeciwnych stronach prostej AB. Za pomocą wzoru na odległość można to zrobić. Tzn obliczyć |AB|, S − punkt wspólny prostych. |AS|, |BS| i porównać jak się te odległości mają do siebie.

Lorak: Może tak: AB:y=0,5x+2 Weźmy sobie jakiś punkt P=(36,y) i zobaczymy dla jakiego y punkt P leży na prostej AB y=0,5*36+2=20, P=(36,20) K=(36,21), czyli leży ponad prostą AB.

Eta:

	1
AB: y=		x+2
	2

21> 18+2 −−− zatem K leży nad tą prostą −15 < −13,5 −−− zatem L leży pod tą prostą Wniosek:............

RS: skąd wiadomo, że te punkty leża nad prostą ?

Eta: O kurczę spóźniłam się ( bo robiłam w tym czasie herbatką

Eta: k: y> ax+b to P(x,y) leży nad prostą

RS: herbatkę z ''prądem'' ?

RS: Eta jesteś jeszcze na forum ?

ZKZ: Dobry wieczor . Chcialbym zwrocic uwage na na okreslenie autora zadania czyli [C[po tej samej stronie prostej]] Otoz wydaje mi sie ze jest to nieprawidlowe okreslenie . Dlaczego? Linia nie moze posiadac szerokosci .Czesci linii moga byc mierzone i porownywane pod wzgledem dlugosci . Dlatego okreslenie po tej samej stronie sugeruje wedlug mnie ze prosta posiada szerokosc a tak nie jest. Dlatego wedlug nie prawodlowe powimno byc okreslenie czy te punkty leza nad prosta czy pod prosta ? jesli jestem w bledzie to prosze mnie poprawic

RS: Zadanie jest dobrze sformułowane.

ZKZ: Moze inaczej . Zadanie jest dobrze przepisane ale czy dobrze sformulowane ?

Rafał28: Zadanie jest chyba na poziomie licealnym. Wchodzenie w aż tak drobne szczegóły mija się z celem. Na przykład tutaj autor używa strona prostej http://www.math.us.edu.pl/pgladki/faq/node102.html W innych zadaniach używają pod, nad prostą.

ZKZ: czesc Rafal28 Przyjmuje to do wiadomosci ze tak moze byc Jednak to nie sa tak drobne szczegoly bo od tego wlasnie zaczyna sie nauka geometrii czyli pojecia punktu ,linii , prostej .

ZKZ: Oczywiscie jak pojec pierwotnych zapomnialem dopisac

RS: Wyznacz współrzędne punktu P , który dzieli odcinek o końcach A=(29,−15) i B=(45,13) w stosunku |AP| : |PB|= 1:3 |AB|=√29−45)²+(−15−13)² |AB|=4√65 |AP|=√65 Jak teraz podstawić pod wzór na długość odcinka aby wyznaczyć współ ?

Rafał28: Cześć. W takim razie popatrzmy. Prosta, pewna linia, która nie ma szerokości ani pola. Myślę, że potocznie można powiedzieć, że ma stronę lewą i prawą, chociaż ciężko ustalić, która to lewa . Sformułowanie pod, nad jest lepsze, ale co w przypadku, gdy mamy k: x=2.

RS: ?

Eta: → → AB= 4AP ⇒ [28,16]= 4*[x−29, y+15] ⇒ x=.... y=....

RS: <kocham> wektory a bez nich jak to zrobić ?

ZKZ: Lub skorzystac z okreslenia rownosci dwoch wektorow i mamy wtedy

	1
AP=		PB tam maja byc strzalki
	3

Eta: Nie lubię ułamków

ZKZ: Jeden lubi kwiaty a drugi corki ogrodnika

	x1+kx2		y1+ky2		1
Albo niech policzy ze wzorow x=		i y=		gdzie k=
	1+k		1+k		3

Eta: Oooo .... ten wzorek tak

ZKZ: A tak nawiasem mowiac to sa one jeszcze w tablicach maturalnych?

Eta: https://matematykaszkolna.pl/forum/229858.html

ZKZ: No to ja

ZKZ: https://matematykaszkolna.pl/forum/229858.html tu napisalem wyjasnienie problemu

RS: Jak zrobić to bez wektorów. ?

RS: ?

Kaja: popatrz na rozwiązanie Ety z 3 stycznia.

RS: ale chodzi o to drugie zadanie z 4 stycznia

RS: ?

Kaja: zrób to wg. własnego pomysłu, czyli podstaw pod wzór na długość odcinka (ale dla |AP| i dla |BP|). będą dwie niewiadome,więc potrzebujesz dwóch równań

ZKZ: Powiem tak . Jesli chcesz zrobic to bez wektorow to zapoznaj sie ze wzorami z godz 1:17 ktore zreszta potwierdzila Pani Eta . Inaczej Punkt P ma wspolrzedne P(x ,y) (patrz rysunek 1:03 i post 1:08)

	1
AP=		PB to
	3

	1
[x−29, y+15]=		[45−x,13−y] wobec rownosci zapisz tak
	3

	1
x−29=		(45−x) to x= juz sobie policzysz
	3

	1
y+15=		(13−y) to y= tez policz
	3

Teraz tez zrob to zadanie sposobem Pani Ety Czyli tak AB=4AP wedlug mnie powinno byc [16,28]=4*[x−29 , y+15] 16=4(x−29) i 28=4(y+15) 3. Tak jak chcesz . Policz dlugosc odcinka AB ( zapisuj porzadnie tak jak ma byc )i sprawdz

	1
swoje obliczenia.		dlugosci odcinka AB to dlugosc odcinka AP .
	4

Teraz zostawiam te obliczenia TObie do zrobienia . x=x₁+wyliczona dlugosc AP czy tez da poprzednio wyliczne x to samo y=y₁+dlugosc odcinka AP czy tez da poprzednio wyliczone y Wedlug mnie tak chciales to zrobic . Wiec jesli wyjdzie dobrze to masz swoj sposob a jesli nie to liczysz tymi wyzej .

ZKZ: Dzien dobry Pani Eto prosze spojrzec na post z 2:46. Czy takie wyjasnienie wystarczy Pani ?

Eta: Witam Pana ZKS

Eta: ZKZ ? od kiedy ?

ZKZ: Pani Eto Ja naprawde nie jestem ZKS . Prosze mnie z nim nie mylic . Z tego co przeczytalem na forum i przgladajac archiwum zanim sie zarejestrowalem to ZKS jest studentem a Pani pisuje juz tu od 2009r. . Majac to na wzgledzie dlatego przy calym szacunku tego co Pani robi pisze Pani

RS: ZKZ to 5−latek ten sam styl pisania. Tylko nie wiem czemu nick zmienił ?

ZKZ: Mylisz sie kolego . Ja nie jestem 5−latek . Owszem znam go osobiscie bo to jest moj rodzony brat Krzysiek Razem korzystamy z tego komputera wiec niekiedy uzywam raz tego nicku albo nicku 5−latek .

RS: Hmm..