pl RS: Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: P = (1,3), Q =(−5,4), R=(−6,7) Wiem, że trzeba stworzyć dwa układy równań z 3 niewiadomymi. Ale które punkty dobrać do siebie P=(x_A,y_A) Q=(x_B,y_B) R=(x_C,y_C) ?

5-latek: https://matematykaszkolna.pl/forum/229195.html

RS: Wiem o tym ale ja nie wiem jak dobrać te punkty.

5-latek: Zrob rysunek z zaznaczeniem punktow PQR i oznaczeniem wierzcholow trojkata A B C wzoruj sie na rysunku utem

Saizou : wzór na środek odcinaka np.

	xa+xb		ya+yb
(1,3)=(		;		)
	2		2

i tak dalej

RS: A Ty przeczytałeś o to co ja pytałem ? Nie chodzi mi o rozwiązanie utem (wektory) tylko rozwiązanie Bogdana ale nie wiem jak zbudować układ równań i w tym mam problem.

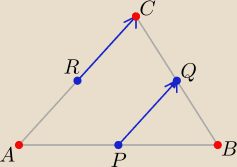
devo: → → PQ=[−7,4] = RC ⇒ C(−6−7, 7+4) A(2x_R−x_C, 2y_R−y_C)=..... i reszta podobnie ....... działaj

RS:

	xa+xc		ya+yc
Ale czemu nie dajesz np (		,		?
	2		2

RS: A bez wektorów. ?

Saizou : a to tylko tak przyjmujesz, bo jakiś sposób zapisu musi być, zresztą jak się posłużysz moim rysunkiem to widziesz, że to co napisałeś to środek odcinak lACl, czyli punkt R

devo: x_A+x_C= 2x_R=2*(−7) ... podobnie dla y−ków x_A+x_B= 2x_P =... x_B+x_C= 2*x_Q=... trzy niewiadome, trzy równania i ......... leć

devo: To jest przekształcony wzór na współrzędne środka odcinka

	xA+xC
bo xR=		⇒ xA+xC= 2xR
	2

RS: OK dzięki devo