m RS: Dane są punkty: A=(9,3) B=(1,3) C=(3,9) są one środkami boków trójkąta znajdź wierzchołki tego trójkąta. Na maturze próbnej roz było podobne i też poległem na nim. Proszę o wytłumaczenie.

AS: Wykorzystaj wzór na środek odcinka,ułóż trzy równania i je rozwiąż.

RS: A koniecznie trzeba męczyć się układem ? Nie można jakoś sprytnie tego obejść ?

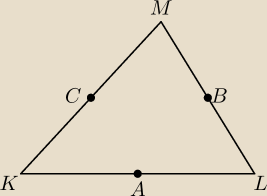
Bogdan: K(x_K, y_K), L(x_L, y_L), M(x_M, y_M) A(9, 3), B(1, 3), C(3, 9) Trzeba rozwiązać dwa układy równań: pierwszy z niewiadomymi x_K, x_L, x_M oraz drugi z niewiadomymi y_K, y_L, y_M. x_K + x_L = 2*9 x_L + x_M = 2*1 x_M + x_K = 2*3 oraz y_K + y_L = 2*3 y_L + y_M = 2*3 y_M + y_K = 2*9

RS: Dzięki, Pomyślę jeszcze nad tym zadaniem.

Bogdan: Pokażę rozwiązanie pierwszego układu: x_K = 18 − x_L i x_M = 2 − x_L i 2 − x_L + 18 − x_L = 6 ⇒ 2x_L = 14 x_L = 7 i x_K = 18 − 7 = 11 i x_M = 2 − 7 = −5

MQ: Można jeszcze tak: BK^→=BC^→+BA^→ i analogicznie pozostałe. Ale, szczerze mówiąc, nie wiem, czy to szybsza i wygodniejsza metoda

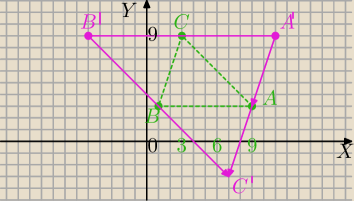
utem: A(9, 3), B(1, 3), C(3, 9) Odcinek łączący środki dwóch boków Δ jest równoległy do boku trzeciego i równy jego połowie AB^→=[−8,0] C=(3,9)→T_[−8,0]→B'=(3−8,9+0]=(−5,9) C=(3,9)→T_[8,0]→A'=(3+8,9+0]=(11,9) CB^→=[−2,−6] A=(9,3)→T_[−2,−6]→C'=(9−2,3−6)=(7,−3)

RS: utem fajnie rozwiązałeś, ale ja jestem zielony z wektorów.

5-latek: A wiesz jakie twierdzenie wykorzystala Mila Pozdrawiam i ?

RS: A co mi daje twierdzenie skoro do tego trzeba znać świetnie wektory ?

5-latek: No skoro nie znasz tweirdznia o linni srodkowej trojkata to poczytaj sobie o nin OK?

RS: ok

pigor: ..., A=(9,3) B=(1,3) C=(3,9) są środkami boków ΔMKL;znajdź jego wierzchołki. −−−−−−−−−−−−−−−−−−−−−−−−−− lub tak: (BC^→|| LK i A∊LK) i (CA^→|| ML i B∊ML) i (AB^→|| KM i C∊KM) ⇒ ⇒ ( [2,6] || LK i (9,3)∊LK) v ( [6,−6] || ML i (1,3)∊ML) v ( [−8,0] || KM i (3,9)∊KM) ⇒ ⇒ ( 2[1,3] || LK i (9,3)∊LK) v ( 6[1,−1] || ML i (1,3)∊ML) v ( 8[−1,0] || KM i (3,9)∊KM) ⇒ ⇒ ( [3,−1] ⊥ LK i (9,3)∊LK) v ( [1,1] ⊥ ML i (1,3)∊ML) v ( [0,1] ⊥ KM i (3,9)∊KM) ⇒ ⇒ 3(x−9)−1(y−3)=0 v 1(x−1)+1(y−3)=0 v 0(x−3)+1(y−9)=0 ⇔ ⇔ LK: 3x−y−24=0 v ML: x+y−4=0 v KM: y−9=0 − równania boków ΔMKL, zatem szukane wierzchołki, to rozwiązania 3−ech układów równań: L (3x−y=24 i x+y=4) v M (x+y=4 i y=9) v K (3x−y=24 i y=9) ⇔ ⇔ L: (4x=28 i y=4−x) v M: (x=4−9 i y=9) v K: (3x=33 i y=9) ⇔ ⇔ L: (x=7 i y= −3) v M: (x= −5 i y=9) v K: (x=11 i y=9) ⇔ ⇔ L=(7,−3) v M=(−5,9) v K=(11,9) − szukane wierzchołki Δ . ...