l
madzia:
mam wyznaczyć taką prostą przez takie punkty A=(−2,3) B=(−2,0)
−2a+b=3
−2a+b=0
=−3
28 gru 23:27
madzia: ?
28 gru 23:36
28 gru 23:39
Maslanek: mhm

28 gru 23:39
madzia:
ale tu nic nie wychodzi

mam układ równań
−2a+b=3 /−1
−2a+b=0
2a−b=−3
2a+b=0
i co wyszło ?
28 gru 23:41
Eta:
Jeżeli xA= xB to prosta AB: x= xA
czyli AB: x= −2
28 gru 23:50
28 gru 23:51
agulka: A=(−2,3) B=(−2,0)
x1=−2
y1=3
x2=−2
y2=0
i to podstawiasz do wzoru: (x2−x1)(y−y1)=(y2−y1)(x−x1)
28 gru 23:52
Ajtek:
Eta a dlaczego nie x=x
B

28 gru 23:53
Eta:

28 gru 23:54
Eta:
x= x
A=x
B = −2 ( ja lubię A

28 gru 23:55
madzia:
Dziękuję
28 gru 23:55
Ajtek:
To lubisz
Ajtka 
28 gru 23:56
Eta:
Dokładnie

28 gru 23:57
madzia: a jeśli już jest taka prosta y=−2 i punkt A(−2,−1,5) to prostopadła jakie ma współrzędne ?
28 gru 23:58
28 gru 23:58
Eta:
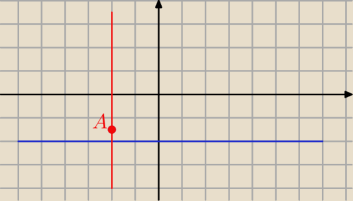 x=−2
x=−2
29 gru 00:00
madzia: dziękuję
29 gru 00:15
Eta:

29 gru 00:18
pigor: ..., wyznaczyć prostą przez takie punkty
A=(−2,3) B=(−2,0)
−−−−−−−−−−−−−−−−−−−−−−−−−−−−
o

i tu właśnie widać wyższość prostej w postaci Ax+By+C=0,
choć ...

takie proste wyznacza się w pamięci, a
więc
AB
→=[ −2+2,0−3]= [0,−3] ⇒ 3x+0*B+C i 3*(−2)+0+C=0 ⇒
⇒ C= 6 i 3x+6= 0 /:3 ⇒
x+2=0 − szukane
równanie prostej AB
29 gru 01:36
Gustlik: Madziu, układ to najdłuższa i jedna z najtrudniejszych metod na tego typu zadanie. To się
robi wektorami.
A=(−2,3)
B=(−2,0)
AB
→=[−2−(−2), 0−3]=[0, −3]
| | −3 | |
Współczynnik kierunkowy a= |
| → nie istnieje. |
| | 0 | |
Mamy więc prostą pionową o równaniu x=−2 (bo oba punkty mają taką współrzędną x).
29 gru 12:56

 mam układ równań
−2a+b=3 /−1
−2a+b=0
2a−b=−3
2a+b=0
i co wyszło ?
mam układ równań
−2a+b=3 /−1
−2a+b=0
2a−b=−3
2a+b=0
i co wyszło ?







 i
i 
 .
.
 x=−2
x=−2

 i tu właśnie widać wyższość prostej w postaci Ax+By+C=0,
choć ...
i tu właśnie widać wyższość prostej w postaci Ax+By+C=0,
choć ...  takie proste wyznacza się w pamięci, a
więc
AB→=[ −2+2,0−3]= [0,−3] ⇒ 3x+0*B+C i 3*(−2)+0+C=0 ⇒
⇒ C= 6 i 3x+6= 0 /:3 ⇒ x+2=0 − szukane równanie prostej AB
takie proste wyznacza się w pamięci, a
więc
AB→=[ −2+2,0−3]= [0,−3] ⇒ 3x+0*B+C i 3*(−2)+0+C=0 ⇒
⇒ C= 6 i 3x+6= 0 /:3 ⇒ x+2=0 − szukane równanie prostej AB