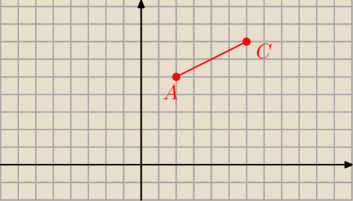
G RS: W układzie współrzędnych na płaszczyźnie punkty A = (2,5) i C = (6,7) są przeciwległymi wierzchołkami kwadratu ABCD . Wyznacz równanie prostej BD |AC|=2√5−przekątna kwadratu 2√5=a√2 a=√10 Czy to będzie prosta prostopadła do prostej AC i przechodząca przez środek AC ? Może jakieś inne pomysły ?

Kaja: tak. wyznacz środek odcinka AC ( z odpowiedniego wzorku) i równanie prostej AC (a przynajmniej jej współczynnik kierunkowy), potem prostą prostopadła do AC i przechodzącą przez jej środek.

tom: Dokładnie tak jak myślisz ( Twoje obliczenia są tu zbędne

	yC−yA
S(4,6) aAC=		= ...
	xC−xA

	1
aBC= −		=...
	aAC

BC: y= a_BC(x−x_S)+y_S=.....

RS: A jak to zrobić za pomocą wektorów. Przyznam że ich jeszcze nie znam a na rozszerzeniu obowiązują.

RS: @Tom, wiem, że moja obliczenia są zbędne ale pierwsza myśl to właśnie taka. Nie wstawiam zadań nie zaczętych i nie liczę na gotowca, bo to nie mój styl. Więc zgodnie z powiedzeniem ''Lepszy rydz..

tom:

RS: A teraz proszę, jeśli masz czas to pokaż jak zrobić to na wektorach ? (Do 100% z roz i podstawy brakuje mi tylko analitycznej ) !

RS: I jeszcze poproszę o jakiś link do przyspieszonej nauki wektorów.

tom: → S(4,6) AS=[2,1] BC : 2*x+1*y+C=0 i S(4,6) ⇒ C= −14 BC: 2x+y−14=0

RS: A możesz bardziej to rozpisać ?

tom: https://matematykaszkolna.pl/strona/1214.html

RS: @Tom też w tym roku masz maturę ?

tom: Dopiero za 2 lata

RS: Wow