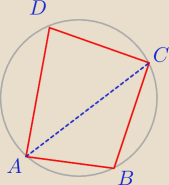
Planimetria Radek: Na czworokącie ABCD można opisać okrąg. Oblicz długości przekątnej AC, jeżeli AB=10 BC=3 CD=6 AD=5 Nie mam pomysłu na to. Proszę o jakąś wskazówkę

Saizou : twierdzenie Carnota w dwóch ujęciach xd

zvx: |<D|= α i |<B|= 180^o−α dwa razy tw, kosinusów

Saizou : Radek spasuje trochę chociaż na święta

zvx: Walczy o 100% z rozszerzenia w maju

Saizou : do maja jeszcze długo

Radek: I szybko się nie poddam ! Trzeba nadrobić planimetrię i analityczną

Radek: @zvx też myślałem, żeby tak zrobić: dwa razy twierdzenie cosinusów ale s wychodziło z cosα

zvx: cos(180^o−α) = −cosα teraz próbuj dokończyć

Saizou : dokładnie to samo napisałem a tego już nikt nie widzi

Radek: Ale ja znam wzory redukcyjne

zvx: s²=25+36−30cosα i s²=100+9+30cosα dodaj stronami i...........

Radek: 2s²=170 s²=85 s=√85 Tylko jak na to wpaść, że akurat trzeba to dodać stronami ?

Saizou : możesz też rozwiązać układ równań ale po co potrzeba nam tylko s, a cosx ładnie się redukuje przy takich liczbach xd

Radek: Hmmm.

zvx: Dodając stronami pozbywasz się cosinusa

zvx: Można i tak ( jak już bardzo chcesz) z pierwszego równania −30cosα= s²−61 do drugiego równania s²=109−s²+61 ⇒ s=.....

Radek: Już zrobiłem na podstawie postu 18:40. Po prostu miałem problem bo s wychodziło mi z cosinusem i nie wiedziałem, że trzeba dodać to stronami. A na pamięć nie chcę się uczyć, tylko to zrozumieć..

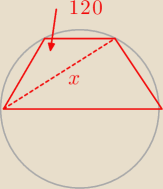
Radek: Na trapezie równoramiennym o kącie ostrym 60⁰ opisano okrąg o promieniu 2. Jedna z podstaw jest średnicą tego okręgu. Oblicz pole tego trapezu

x
	=2R
sin120

x
	=4
√3   2

	2
d*		=4
	√3

2√3d
	=4
3

2√3d=12 d=2√3 Ale co dalej ?

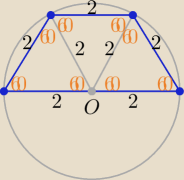
zvx: P(tr)= 3*P(Δrównobocznego)= ....

Radek: ?

Radek: A skąd wiadomo, że promienie podzielą go na 3 trójkąty równoboczne ?

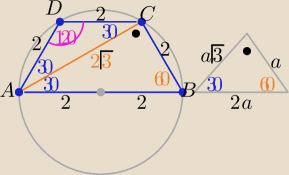
zvx: 2 sposób P(ABCD)= P(trójkataABC)+P(trójkątaACD) = .......

Radek:

Radek: ?

Radek: ?

Radek: Czemu tam przy górnej podstawie jest kąt 90⁰ ?

5-latek: A kat wpisany oparty na srednicy = ile stopni?

Radek: 90⁰ a pytanie 19:15 ?

zvx: https://matematykaszkolna.pl/strona/465.html

Radek: Ale ja się pytam o pierwszy sposób

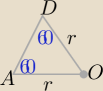
zvx: Trójkąt ADO równoramienny o ramionach "r" i kącie A= 60^o to.........

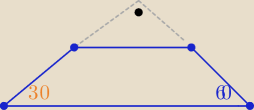
Radek: A np mam taki trapez czy tu przekątna też będzie do ramienia przy górnej podstawie tworzyła kąt prosty ?

zvx:

Radek: Czyli tylko w trapezie równoramiennym jest taka własność ?

zvx: Tylko wtedy.. gdy dolna podstawa zawiera się w średnicy okręgu opisanego na tym trapezie

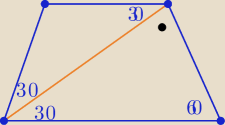
zvx: lub gdy przekątna trapezu równoramiennego o kącie ostrym 60^o zawiera się w dwusiecznej kąta ostrego

Radek: Czyli musi być trapez równoramienny o kącie ostrym 60^o ?

Radek: I jeszcze czemu górna podstawa to 2 przecież stosunek podstaw może być 1:3 ?

BoosterXS: Z punktu O masz poprowadzone 2 promienie tego okręgu do 'górnej' podstawy. Każdy z nich równy 2. Więc masz Δ równoramienny z kątami o mierze 60stopni przy podstawie, a taki trójkąt(180−60−60=60) jest równoboczny, więc podstawa ma miarę równą promieniowi(ramionom) Coś pomogłem?

Radek: Coś tak.

BoosterXS: Radek, która klasa?

Radek: 3 lo

zvx: czyt. post 20:02

BoosterXS: to tak jak ja, rozszerzoną piszemy?

Radek: Tak.

Radek: I mi właśnie o to chodzi, że skąd wiadomo, że ramie ma długość promienia ?

BoosterXS: no to trzeba działać ostro ; ) a co oprócz matmy i jakie studia wstępnie?

zvx: No przecież okrąg opisany na trapezie

BoosterXS: Kurcze...Radek. Bo rozszerzonej nie zdasz. Jak ze środka prowadzisz odcinek do punktu znajdującego się na okręgu to chyba logiczne, ze musi się on równać promieniowi

Radek: Fizyka i angielski roz. Wojskowa Akademia Techniczna−Automatyka i robotyka a Ty ? @zvx ?

zvx:

BoosterXS: Gegra R, ang R i ruski P, a chciałbym na SGH w Warszawie

Radek: Ja fizyka roz oczywiście I nie bój się o moją maturę zdam ją !

zvx: