Szukanie parametru czopo: Witam, mam problem z zadaniem, nie mam pojęcia jak się zabrać za tego typu zadanie... Dla jakich wartości parametru m rozwiązaniem układu równan: my − 9x = −4 mx − y = m jest para liczb (x,y) spełniająca nierówność x + y ≥ 1 ? Wesołych świąt

Piotr 10: Proponuję metodę wyznaczników

Piotr 10: Więcej o niej tutaj https://matematykaszkolna.pl/strona/1192.html

czopo: Coś musiałem zepsuć. Tą metodą wyszło mi m ≥ 1, gdzie wynikiem ma być m∊(−3;−1> ∪ (3;∞)

5-latek: To pokaz jak liczyles

Święty Mikołaj: y = mx − m m²x − m² − 9x = −4, x(m² − 9) = m² − 4 i m≠−3 i m≠3

	m2 − 4		m2 − 4		5m
x =		i y = m*		− m =
	m2 − 9		m2 − 9		m2 − 9

m2 − 4		5m		m2 + 5m − 4
	+		≥ 1,		− 1 ≥ 0
m2 − 9		m2 − 9		m2 − 9

5(m + 1)
	≥ 0 ≡ 5(m + 1)(m − 3)(m + 3) ≥ 0
(m − 3)(m + 3)

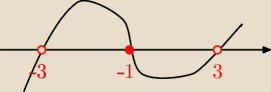
m∊(−3, −1>∪(3, +∞)

czopo: Zrobiłem metodą wyznaczników i wyszło mi, ze W = 9 − m², Wx = 4 − m² a Wy = −5m Podstawiłem to to wyszło, że X = ^4−m2_9−m² a Y = ^−5m_9−m² Następnie do równania x + y ≥ 1 podstawiłem te dwie wartości i mi tak wyszło. Nie wiem, gdzie jest błąd.

czopo: Dobra, chyba wiem, gdzie był błąd, ale nie wiem, dlaczego ma poodwracane znaki kolega, który zrobił wyżej