matematykaszkolna.pl
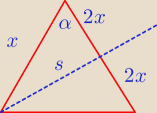
planimetria Radek: rysunek Jeden z kątów trójkąta ma miarę α. Stosunek długości boków zawartych w ramionach tego kąta jest równy 4:1, a środkowa poprowadzona do dłuższego z nich ma długość s. Znajdź długości boków tego trójkąta. Ale co dalej ? Proszę o wskazówki ?
23 gru 16:40
Radek: https://matematykaszkolna.pl/forum/14131.html
23 gru 16:51
Radek: Tylko skąd się wzięło 4a ?
23 gru 16:56
Radek: ?
23 gru 17:36
utem: W górnym Δ stosujesz tw. cosinusów s2=x2+(2x)2−2*x*2x *cosα s2=x2+4x2−4x2*cosα Dokończysz?
23 gru 18:33
Radek: Też tak chciałem policzyć ale wychodzi mi ' s2=5x2−4x2cosα s2=x2(5−4cosα) s=x√5−4cosα) ?
23 gru 18:50
Kaja: podziel przez ten pierwiastek
23 gru 18:51
Radek:
 s 
x=
?
 √(5−4cosα) 
23 gru 18:53
Kaja: tak. a teraz ten drugi bok przy kącie α, to 4x, więc do tego podstaw za x to co wyliczyleś
23 gru 18:54
Kaja: a ten trzeci bok wylicz z Tw. cosinusów
23 gru 18:58
Radek:
4s 
√5−4cosα) 
Ostatni bok z twierdzenia cosinusów też ?
23 gru 18:58
Kaja: tak
23 gru 18:58
Radek:
 4s s 4s s 
y2=(
)2+(
)2−(2*
*
*cosα)
 √5−4cosα) √5−4cosα √5−4cosα √5−4cosα 
23 gru 19:03
Radek:
 16x2 s2 2s2cosα 
y2=
+
−
 5−4cosα 5−4cosα 5−4cosα 
 17s2 2s2cosα 
y2=
−
 5−4cosα 5−4cosα 
 17s2−2x2cosα 
y2=
 5−4cosα 
 x(17−2cosα) 
y=√
 5−4cosα 
23 gru 19:23
Radek: Wszystko wyszło emotka
23 gru 19:25
cicha noc: Sposób "Ety" taki samemotka zamiast "x" oznaczyła "a"
23 gru 21:19
Radek: Jednak wolałem sam do tego dojść niż korzystać z gotowego rozwiązania emotka
23 gru 21:21
cicha noc: emotka
23 gru 21:22
Radek: I przy okazji chciałbym Pani Ecie, Pani Mili, ZKS i Panu Bogdanowi Wesołych Świąt bo jutro nie wiem czy będę na forum.
23 gru 21:24
utem: Wesołych świąt, Radek, baw się dobrze w Sylwestra w miłym towarzystwie.
23 gru 21:31
Eta: Tobie również życzę Wesołych Świąt ( i koniecznie bez matematyki przez dni świąteczne emotka
23 gru 21:32