Planimetria
Radek:
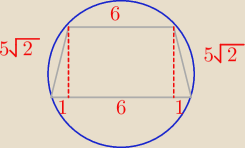
Jak znaleźć promień okręgu opisanego na tym trapezie ?
22 gru 17:28
Radek: ?
22 gru 17:41
ogipierogi: 12+y2=(5√2)2
bedziesz miał długość linii kropkowanej, i wstawiasz go w miejsce y do drugiego równania
(y)2+72=x2
to co wyjdzie przez 2 dzielisz i masz wynik
22 gru 17:46
Radek:
A czemu tak ? Proszę o wytłumaczenie
22 gru 17:49
ogipierogi: przepraszam, popier... rozwiązania, oczywiście zignoruj je, bo trzeba tu skorzystać z
twierdzenia sinusów
22 gru 17:56
utem:
Wskazówka:
Narysuj przekątną.
Promień okręgu opisanego na trapezie ABCD jest równy promieniowi opisanemu na ΔABC.
22 gru 18:03
ogipierogi: 1
2+y
2=(5
√2)
y=7 − wysokość trapezu
obliczam sinus konta między ramieniem a dłuższą podstawą
oblicz długość przekątnej trapezu, oznacze ja jako d,R jako promień
z twierdzenia sinusów
22 gru 18:04
Radek:
Ale jak wyliczyć tę przekątną ?
22 gru 18:09
utem:
Z tw. Pitagorasa.
22 gru 18:15
Radek:
A skąd wiadomo, że tam jest kąt prosty ?
22 gru 18:20
utem:
d2=72+h2
22 gru 18:30
Radek:
A jak inaczej to wywnioskować ? Czy w innych trapezach zawsze jest kąt prosty
22 gru 18:32
utem:
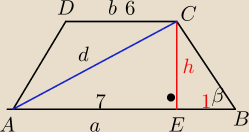
CB=5
√2
(5
√2)
2=h
2+1
h
2=49
h=7
d=7√2
Teraz jasne?
Dokończ
22 gru 18:38
22 gru 19:10
Radek:
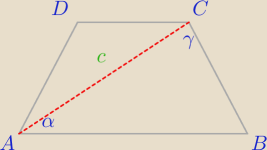
W trapezie równoramiennym ABCD (AB||CD) dane jest: |AC|=c |∠CAB|=α i |∠ACB|=γ. Oblicz długości
boków trapezu
| c | | AB | |
| = |
| |
| sin[180−(α+γ)] | | sinγ | |
csinγ=ABsin(α+γ)
|CB|=|AD|
csinα=CBsin(α+β)
Ale jak wyznaczyć CD ?
22 gru 21:36
cicha noc:
Sprawdź czy dobrze napisałeś treść zadania
22 gru 21:49
bezendu:
| | csin(2α+γ) | |
CD= |
| Resztę masz dobrze. |
| | sin(α+β) | |
22 gru 21:55
cicha noc:
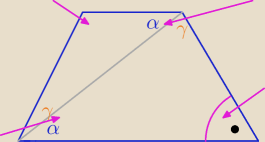
2α+2γ= 180
o ⇒ α+γ= 90
o
ten trapez jest
prostokątem
zatem a= c*sinγ , b= c*sinα
22 gru 22:03
Radek:
prostokątem ? Tam w kropce powinno być 180−(α+γ) ?
22 gru 22:05
cicha noc:
Skoro α+γ= 90
o to jasne,że ..... 180
o−(α+γ)= 90
o
22 gru 22:07
Radek: Czyli w miejscu tej strzałki (lewy górny róg) będzie 180−(α+γ) ?
22 gru 22:09
cicha noc:
We wszystkich rogach kąt prosty
22 gru 22:15
Radek:
| | c | | CD | |
mi CD wyszło tak |
| = |
| |
| | sin(α+γ) | | sinγ | |
22 gru 22:17
Radek: ?
22 gru 23:29
cicha noc:
Zobacz jak Ty to przekształciłeś !
| | c*sinγ | |
to CD= |
| , i ponieważ α+γ= 90o |
| | sin(α+γ) | |
CD= c*sinγ
23 gru 00:02
Radek:
No tak napisałem ? A co jest nie tak w tym zapisie ? Może Pani powiedzieć ?
23 gru 00:04
Radek:
I jeszcze pytanie jak wyzanczyć tg 750 tg(90−15)=−ctg150 jak teraz ctg15
23 gru 00:10
Lorak: tg75o=tg(30o+45o)=...
23 gru 00:24
cicha noc:
1/ wpis
22:17 źle przekształciłeś ( zobacz..)
| | tgα+tgβ | |
tg75o= tg(30o+45o)= ... zastosuj wzór na tg(α+β)= |
| |
| | 1−tgα*tgβ | |
23 gru 00:25
cicha noc:
No i już się "wciął"
Lorak 
23 gru 00:25
Lorak:
to idę spać
23 gru 00:28
cicha noc:
23 gru 00:28
23 gru 00:29
Lorak: dzisiaj już nie dam rady, zasypiam.
dobranoc
23 gru 00:52
5-latek: | | 3+√3 | |
tg75= |
| i po usunieciu niewymiernosci z mianownika =2+√3 |
| | 3−√3 | |
lub tak tg75=ctg15
| | x | | 1+cosx | | √3 | |
ze wzoru polowkowego ctg |
| =√ |
| cos30= |
| i liczysz |
| | 2 | | 1−cosx | | 2 | |
23 gru 09:10
Radek:
Ale w którym momencie jest to źle przekształcone ?
23 gru 15:41
matyk: Masz podane co było źle
23 gru 15:58
Radek: A no tak nie zauważyłem
23 gru 16:02
