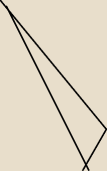
 Dla trójkąta wyznacz promien okręgu wpisanego w ten trójkąt
Wierzchołki kolejno od dolu
A 4i1/2
B 7i1/2
C −5
Dla trójkąta wyznacz promien okręgu wpisanego w ten trójkąt
Wierzchołki kolejno od dolu
A 4i1/2
B 7i1/2
C −5
| 2P | ||
r= | , a,b, c −−− długości boków | |
| a+b+c |
| 1 | ||
P−− pole ( ze wzoru Herona} lub P= | a*b *sin <(a,b) | |
| 2 |
| α | r | |||
Latwiej skorzystac ze wzoru tg | = | gdzie r− promien okregu wpisanego | ||
| 2 | p−a |
| α | (p−b)(p−c) | |||
p−−−−polowa obwodu a tg | =√ | jak nie widac to wszystko jet pod | ||
| 2 | p(p−a) |
 Podrawiam
Podrawiam  Wiem ze podaje wzory ktore juz sie nie stosuje ale moze jeszcze taki
Wiem ze podaje wzory ktore juz sie nie stosuje ale moze jeszcze taki
| α | β | γ | ||||
r=4Rsin | *sin | *sin | gdzie R to promien okregu opisanego −−−− gdzie | |||
| 2 | 2 | 2 |
| α | (p−b)(p−c) | |||
sin | =√ | i analogicznie pozostale katy | ||
| 2 | bc |

 .
.
 wzajemnie .
Zdrowych i wesolych Swiat Bozego Narodzenia Zycze Tobe jak i dla calej rodziny
wzajemnie .
Zdrowych i wesolych Swiat Bozego Narodzenia Zycze Tobe jak i dla calej rodziny Do krystek napisze w wigilie zyczenia
Do krystek napisze w wigilie zyczenia 