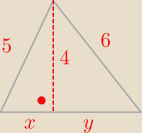
Planimetria Radek: Dwa boki trójkąta ostrokątnego mają długości 5 i 6, zaś wysokość poprowadzona do trzeciego boku ma długość 4. Oblicz promień okręgu opisanego na tym trójkącie. x²=5²−4²=9 x=3 y²=6²−4²=20 y=2√5 Z twierdzenia kosinusów. (3+2√5)²=5²+6²−2*5*6*cosα 29+12√5=25+36−60cosα −32+12√5=−60cosα /(−1) 32−12√5=60cosα 4(8−3√5)=4*15cosα /4 8−3√5=15cosα

	8−3√5
cosα=
	15

	8−3√5
sin2α=1−(		)2=... i tutaj wychodzi pierwiastek pod pierwiastkiem
	15

	64−48√5+45
sin2α=1−
	225

	225−(109−48√5
sin2α=
	225

	116+48√5
sin2α=
	225

Bizon: ... nie łatwiej ze wzoru ? https://matematykaszkolna.pl/strona/541.html

Lorak:

	abc
R=
	4P

do obliczenia pola wszystkie potrzebne dane już masz

Radek: A no tak, można szybciej Dziękuję