matematykaszkolna.pl
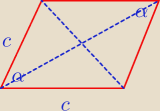
Planimetria Radek: rysunek Wyznacz długości przekątnych rombu o boku c i kącie ostrym α d2=c2+c2−2c2sinα d2=2c2−2c2sinα d2=2c2(1−sinα) d2=c√2(1−sinα) OK ? ta pierwsza
21 gru 22:09
Saizou : źle to jest tw. carnota
21 gru 22:10
Radek: d=c√2(1−cosα) ?
21 gru 22:12
Saizou : teraz ok
21 gru 22:13
Radek: A drugą jak wyliczyć ?
21 gru 22:15
Saizou : a jaki będzie drugi kąt skoro jedne to α ?
21 gru 22:16
Radek: 180−α ? czy β ?
21 gru 22:17
Radek: już wiem dzięki emotka
21 gru 22:17
Saizou : β=180−α emotka zatem....
21 gru 22:17
Saizou : proszę
21 gru 22:18
Radek: f2=c2+c2−(2c2(−cosα)) f2=2c2+2c2cosα f2=2c2(1+cosα) f=c√2(1+cosα) ?
21 gru 22:28
Saizou : odkładnie tak
21 gru 22:28
Saizou : dokładnie
21 gru 22:29
Radek:
 α 
w odpowiedzi mam 2csin
 2 
21 gru 22:30
Radek:
 α 
i 2cos
 2 
21 gru 22:30
Saizou :
 x 
bo 1+cosx=2cos2(
)
 2 
21 gru 22:33
5-latek :
 x 
1+cosx=2cos2
 2 
https://matematykaszkolna.pl/strona/3670.html czwarty wzor od gory
21 gru 22:35
Eta:
 x 
I jeszcze taki 1−cosx= 2sin2
 2 
Często pisałam,że warto te dwa wzorki znać emotka ( albo je wyprowadzić emotka
21 gru 22:37
matyk: Na szczęście jeśli w treści zadania nie ma polecenia jak ma wyglądać odpowiedź to nikt nie ma prawa zarzucić, że masz źle emotka
21 gru 22:39