Planimetria
Radek:
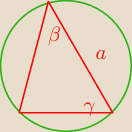
Jeden z boków trójkąta ma długość a, zaś kąty przyległe do niego mają miary α i β.Znajdź pole
tego trójkąta
sin(180−(β+γ)=sin(β+γ)
a=2Rsin(β+γ)
I dalej się zgubiłem
20 gru 19:08
Radek: ?
20 gru 19:25
20 gru 19:27
Eta:
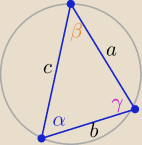
Z tw. sinusów
| b | | a | |
| = |
| ⇒ b=......... |
| sinβ | | sin(β+γ) | |
20 gru 19:28
krystek: I teeraz Radek wybierze.
Eto 
20 gru 19:30
Radek:
Dziękuję Pani Eto. Pani Krystyno nie musi mi Pani podawać linku, bo to znam już na pamięć
!
20 gru 19:33
Eta:
20 gru 19:33
utem:
| b | | b | | a | |
| =2R⇔ |
| = |
| stąd oblicz b, |
| sinβ | | sinβ | | sin(α+β) | |
podobnie trzeci bok, dalej proste
20 gru 19:34
Radek:
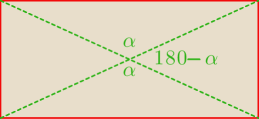
Przekątna prostokąta ma długość d a kat między przekątnymi α, Oblicz obwód tego prostokąta
Jak to zacząć ?
20 gru 19:46
Radek: ?
20 gru 19:58
utem:
Wskazówka:
Przekątne są równe i dzielą się na połowy, wzór na pole Δ z sinα.
20 gru 20:17
Eta:
d
2=a
2+b
2 = (a+b)
2−2ab
d
2=(a+b)
2 −d
2*sinα ⇒ a+b=......... i Ob=....
20 gru 20:21
Radek:
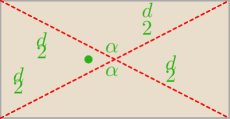
Ale który kąt mam brać 180−α czy α w miejscu kropki 180−α
20 gru 20:22
utem:
sinα=sin(180−α)
20 gru 20:25
20 gru 20:31
Radek:
W ogólne nie rozumiem przekształcenia Pani Ety
d2=a2+b2 to wiem ale d2=a2+b2−2ab po co to ?
20 gru 20:36
Radek: ?
20 gru 20:42
Eta:
(a+b)
2= a
2+2ab+b
2 to rozumiesz?
| | 1 | |
to: a2+b2= (a+b)2−2ab , P=ab i P= |
| d2*sinα |
| | 2 | |
| | 1 | |
d2=(a+b)2 − 2* |
| d2*sinα ⇒ a+b=...... |
| | 2 | |
20 gru 20:44
Radek:
No bez przesady wzór skr.mnożenia rozumiem
a
2+b
2−ab to również rozumiem
ale dalej ani w ząb nie rozumiem
20 gru 20:50
Eta:
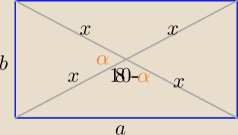
No to
drugi sposób
z tw, cosinusów
d= 2x
b
2= x
2+x
2−2x
2*cosα ⇒ b= ........
a
2= x
2+x
2+2x
2cosα ⇒ a=.....
Ob=......
Tylko nie pisz mi,że i tego nie rozumiesz?
20 gru 20:57
Radek:
Tw cosinusów rozumiem i wole to zastosować
Ale jeszcze pierwszy sposób również muszę
zrozumieć !
20 gru 20:59
Radek:
| | 1 | |
Wracając do pierwszego sposobu P=ab Ale P= |
| d2sinα ? |
| | 2 | |
20 gru 21:04
Eta:
(a+b)
2= a
2+b
2−2ab
za a
2+b
2 =d
2 −−− jasne?
| | 1 | |
i P= ab −−− jasne? i P= |
| *d*d*sinα −−− jasne? |
| | 2 | |
| | 1 | |
to zamiast ab podstawiasz |
| d2*sinα −−− jasne? |
| | 2 | |
otrzymujesz: (a+b)
2= d
2−d
2*sinα −−− jasne?
a+b>0
i dokończ.....
20 gru 21:05
Eta:
Jasne już ?
20 gru 21:09
Radek:
d2sinαcosα ?
20 gru 21:09
Radek: Teraz już jasne, Proste zadania mnie zaginają a trudniejsze potrafię zrobić
20 gru 21:13
Eta:
Będzie dobrze, nabierzesz wprawy rozwiązując kolejne i kolejne i ......
20 gru 21:15
utem:
Możesz obliczyć wysokość jednego z Δ.
20 gru 21:23