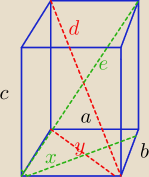
. Piotr 10: Udowodnij, że w każdym równoległościanie suma kwadratów przekątnych równa się sumie kwadratów wszystkich jego krawędzi. Teza: (2d)²+(2e)²=(4a)²+(4b)²+(4c²) Korzystam z twierdzenia, które mówi, że dowolnym równoległoboku suma kwadratów długości przekątnych jest równa sumie kwadratów długości wszystkich boków. x²+y²=2a²+2b² d²=c²+y² e²+c²+x² 4d²+4e²=4c²+4y²+4c²+4x²=8a²+8b²+8c² Co robię źle ?

matyk: Te odcinki, które masz to nie są przekątne równoległościanu Tylko jeden nią jest (który?)

Piotr 10: nie wiem. są chyba 4 przekątne rownoległoscianu. Długości x i y to przekątne równoległoboku

Piotr 10: Ten odcinek e(przekątna) powinna ''zjechać na dół'' jeszcze

matyk: To masz wtedy dopiero 2 przekątne

wodnik: https://matematykaszkolna.pl/forum/167737.html

Panko: rozepnij wektor na krawędziach i zrozumiesz swój kłopot ; lewa strona twojej tezy jest wątpliwa ale wektorowo p₁= a+b+c ; a+b +p₂=c ; p₃= c+a−b ;

Piotr 10: nie rozumiem. mam 4 przekątne w tej figurze

matyk: Zerknij do linka i na rozwiązanie Mili

Piotr 10: Ja idę, bo i tak z tego nic nie rozumiem

Panko: To standardowa metoda do takich rachunków. Przekonaj się na przykładzie charakteryzacji równoległoboku. ( ten fakcik z kwadratami boków i przekątnych) Metody wektorowe ( iloczyn skalarny ) są tu górą. Ogólnie rozpinasz wektorki na krawędziach

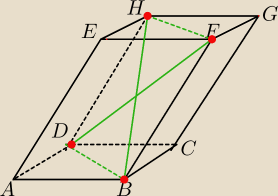
wodnik: Dwie przekątne DF i BH w płaszczyźnie DBFH. Dwie przekątne AG i CE w płaszczyźnie ACGE, nie narysowane, aby nie zaciemniać rysunku.

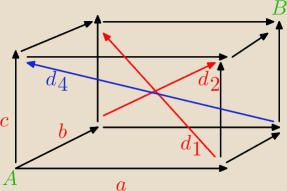
Panko: Kurcze może tak : równości są wektorowe d₁= c−a +b d₂= c+a−b d₃= a+b+c d₄=c−a−b teraz korzystamy z kwadratu skalarnego czyli ( gdzie u to wektor) IuI²= u²=u◯u Id₁I²= d₁²= d₁◯d₁ i analogicznie pozostałe : Id₂I²= d₂²= d₂◯d₂ ........ w zadaniu należy policzyć sumę kwadratów długości przekątnych czyli : Id₁I² +Id₂I² +Id₃I²+Id₄I² przykład policzenia Id₁I²= d₁²= d₁◯d₁ =(c−a +b)◯(c−a +b)=IcI² +IaI² +IbI²−2c◯a−2a◯b+2c◯b przykład policzenia Id₂I²= d₂²= d₂◯d₂ =(c+a −b)◯(c+a −b)=IcI² +IaI² +IbI²+2c◯a−2a◯b−2c◯b itd jeszcze dwa razy. Potem podstawiamy do Id₁I² +Id₂I² +Id₃I²+Id₄I² = ..... i dostajemy żądane Na rysunku brakuje wektora d₃ rozpiętego na przekątnej AB ( od A do B )