awdw
razer: Uzasadnij, że w każdym równoległościanie suma kwadratów przekątnych równa się sumie kwadratów
wszystkich jego krawędzi.
17 lis 18:45
Nienor: Policz długości przekątnych i zobacz, co ci wyjdzie.
17 lis 18:48
razer: wychodzi mi 4a2 + 4b2 + 2h2
przekątne: w podstawie : e i f ; + 2 w calym 2 przekatne (e2+h2) i f2 + h2
17 lis 19:02
razer: podbijam. gdzie popelniam blad
17 lis 19:26
razer: Uktnalem w tym zadaniu, prosze o wskazkowki
17 lis 20:09
Eta:
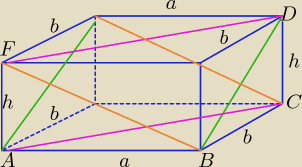
|AC|
2= a
2+b
2 , |BF|
2=a
2+h
2, |BD|
2=b
2+h
2
2|AC|
2+ 2|BF|
2+2|BD|
2= 2(a
2+b
2)+2(a
2+h
2)+2(b
2+h
2)= ......
17 lis 20:45
razer: Mamy przekątną AC pomnozona przez 2 = rozumiem ze to z dolnej i gornej podstawy, ale co z druga
przekotna w dolnej i gornej podstawie ? Co z przekatna |AD| ?
17 lis 21:08
razer: halooooo
17 lis 23:30
razer:
17 lis 23:50
Mila:
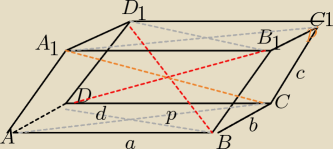
W równoległościanie wszystkie ściany są równoległobokami.
ABCDA
1B
1C
1D
1 jest równoległościanem
Teza: DB
1+BD
1+AC
1+A
1C=
4a2+4b2+4c2 ? ?
ABCD Przystające do A
1B
1C
1D
1
∡A=∡C i ∡B=180−∡C=180−cosA
d
2=a
2+b
2−2abcosA
p
2=a
2+b
2−2abcosB=a
2+b
2+2abcosA (cosinus kąta rozwartego jest ujemny)
(d2+p2)=(2a2+2b2) suma przekatnych podstawy
DB
12=d
2+c
2−2dccos∡DBB
1
BD
12=d
2+c
2−2bdcosDDB=d
2+c
2+2dccos∡DBB
1
DB12+BD12=2d2+2c2
AC
12=p
2+c
2−2pccosAA
1C
A
1C
2=p
2+c
2−2pccosA
1C
1C Jeden z tych katów jest rozwarty
AC
12+A
1C
2=2p
2+2c
2
suma przekątnych =2d
2+2c
2+2p
2+2c
2=
=2d
2+2p
2+4c
2=4a
2+4b
2+4c
2 cnw.
18 lis 01:01
 |AC|2= a2+b2 , |BF|2=a2+h2, |BD|2=b2+h2
2|AC|2+ 2|BF|2+2|BD|2= 2(a2+b2)+2(a2+h2)+2(b2+h2)= ......
|AC|2= a2+b2 , |BF|2=a2+h2, |BD|2=b2+h2
2|AC|2+ 2|BF|2+2|BD|2= 2(a2+b2)+2(a2+h2)+2(b2+h2)= ......
 W równoległościanie wszystkie ściany są równoległobokami.
ABCDA1B1C1D1 jest równoległościanem
Teza: DB1+BD1+AC1+A1C=4a2+4b2+4c2 ? ?
ABCD Przystające do A1B1C1D1
∡A=∡C i ∡B=180−∡C=180−cosA
d2=a2+b2−2abcosA
p2=a2+b2−2abcosB=a2+b2+2abcosA (cosinus kąta rozwartego jest ujemny)
(d2+p2)=(2a2+2b2) suma przekatnych podstawy
DB12=d2+c2−2dccos∡DBB1
BD12=d2+c2−2bdcosDDB=d2+c2+2dccos∡DBB1
DB12+BD12=2d2+2c2
AC12=p2+c2−2pccosAA1C
A1C2=p2+c2−2pccosA1C1C Jeden z tych katów jest rozwarty
AC12+A1C2=2p2+2c2
suma przekątnych =2d2+2c2+2p2+2c2=
=2d2+2p2+4c2=4a2+4b2+4c2 cnw.
W równoległościanie wszystkie ściany są równoległobokami.
ABCDA1B1C1D1 jest równoległościanem
Teza: DB1+BD1+AC1+A1C=4a2+4b2+4c2 ? ?
ABCD Przystające do A1B1C1D1
∡A=∡C i ∡B=180−∡C=180−cosA
d2=a2+b2−2abcosA
p2=a2+b2−2abcosB=a2+b2+2abcosA (cosinus kąta rozwartego jest ujemny)
(d2+p2)=(2a2+2b2) suma przekatnych podstawy
DB12=d2+c2−2dccos∡DBB1
BD12=d2+c2−2bdcosDDB=d2+c2+2dccos∡DBB1
DB12+BD12=2d2+2c2
AC12=p2+c2−2pccosAA1C
A1C2=p2+c2−2pccosA1C1C Jeden z tych katów jest rozwarty
AC12+A1C2=2p2+2c2
suma przekątnych =2d2+2c2+2p2+2c2=
=2d2+2p2+4c2=4a2+4b2+4c2 cnw.