PRAWDOPODOBIEŃSTWO Hajtowy: SPRAWDZIAN PRAWDOPODOBIEŃSTWO Proszę bardzo o sprawdzenie Zadanie 1 Ile jest liczb trzycyfrowych o różnych cyfrach: a) nieparzystych [Moja odp. 405] b) większych od 483 [Moja odp. 463] Zadanie 2

	2		1		1
Oblicz P(A∪B) jeśli P(A')=		, P(B)=		, P(A∩B)=
	3		3		6

	3		1
[Moja odp.		=		]
	6		2

Zadanie 3 Ze zbioru {4,5,6,8,9} losujemy dwie liczby ze zwracaniem tworząc liczbę dwucyfrową. Jakie jest prawdopodobieństwo, że wylosowana liczba:

	15		3
a) będzie parzysta [Moja odp.		=		]
	25		5

	8
b) podzielna przez 3 [Moja odp.		]
	25

Zadanie 4 Na ile sposobów możemy postawić 5 książek na półce obok siebie tak, aby książki ABC stały obok siebie w dowolnym porządku? [Moja odp. 3! * 3! = 6 * 6 = 36] Zadanie 5 Ze zbioru Z={−3;−2;−1;0;1;2;3;4} losujemy liczbę a. Jakie jest prawdopodobieństwo, że ciąg

	3
(		, a , 6) będzie ciągiem geometrycznym?
	2

	2		1		1
[Po sprawdzianie dowiedziałem odp i ma być to		=		− ja napisałem		]
	8		4		8

Zadanie 6 W I urnie jest 3 kule czarne i 7 niebieskich w II urnie 4 czarne i 5 niebieskich. Z każdej urny wyciągamy 1 kulę. Jakie jest prawdopodobieństwo, że kule będą różnych kolorów?

	47
[Moja odp.		]
	90

Zadanie 7 Twinky Winky ma trzy torebki: czaerwoną, zieloną i żółtą. Do torebek zamierza włożyć cztery różne zdjęcia Pani Ewy a) Na ile sposobów może rozmieścić zdjęcia w swoich torebkach? [Moja odp. 3⁴ = 81] b) Na ile sposobów może rozmieścić zdjęcia tak, aby w zielonej torebce nie znalazło się żadne zdjęcie? [Moja odp. 2⁴ = 16] Zadanie 8 Rzucamy dwa razy kostką sześcienną. Jakie jest prawdopodobieństwo zdarzenia, że:

	16		4
a) iloczyn wyrzuconych oczek jest mniejszy od 9 [Moja odp.		=		]
	36		9

	5
b) suma wyrzuconych oczek wynosi 8 [Moja odp.		]
	36

Proszę bardzo o sprawdzenie

Piotr 10: Zad.5 Ze zbioru Z={−3;−2;−1;0;1;2;3;4} losujemy liczbę a. Jakie jest prawdopodobieństwo, że ciąg ( 1,5 ; a ; 6 ) będzie ciągiem geometrycznym? a²=9 a = 3 v a= −3 IΩI=8 IAI=2 , bo zdarzeniem sprzyjającym będzie cyfra 3 lub cyfra −3

	2		1
P(A)=		=
	8		4

Hajtowy: No właśnie Piotrze ... Skapnąłem się po fakcie o tym błędzie tragicznym... A reszta jak?

Piotr 10: W I urnie jest 3 kule czarne i 7 niebieskich w II urnie 4 czarne i 5 niebieskich. Z każdej urny wyciągamy 1 kulę. Jakie jest prawdopodobieństwo, że kule będą różnych kolorów?

	10 1		9 1
IΩI=		*		=90

	3 1		5 1		7 1		4 1
IAI=		*		+		*		=15+28=43

	43
P(A)=
	90

Piotr 10: Twinky Winky ma trzy torebki: czerwoną, zieloną i żółtą. Do torebek zamierza włożyć cztery różne zdjęcia Pani Ewy a) Na ile sposobów może rozmieścić zdjęcia w swoich torebkach? W₃⁴=3⁴=81 b)Na ile sposobów może rozmieścić zdjęcia tak, aby w zielonej torebce nie znalazło się żadne zdjęcie? W₂⁴=2⁴=16

Hajtowy: W I urnie jest 3 kule czarne i 7 niebieskich w II urnie 4 czarne i 5 niebieskich. Z każdej urny wyciągamy 1 kulę. Jakie jest prawdopodobieństwo, że kule będą różnych kolorów?

3		4		7		5		12		35		47
	*		+		*		=		+		=
10		9		10		9		90		90		90

Ja to tak rozwiązałem...

Piotr 10: Rzucamy dwa razy kostką sześcienną. Jakie jest prawdopodobieństwo zdarzenia, że: a) iloczyn wyrzuconych oczek jest mniejszy od 9 Ω=6*6=36 Ω − zbiór 2−elementowych wariacji z powtórzeniami zbioru 6−elementowego A={ (2,5) ; (2,6) ; (3;3); (3;4) ; (3;5) ; (3;6) ; (4;3) ; (4;5) ; (4;6) ; (5;2) ; (5;3) (5;4) ; (5;5) ; (5;6) (6;2); (6;3) : (6;4) ; (6;5) ; (6;6} IAI=19

	19
P(A)=
	36

Piotr 10: b) suma wyrzuconych oczek wynosi 8 A= { (2,6} ; (3;5} ; (4;4) ; (5;3) ; (6;2)}

	5
P(A)=
	36

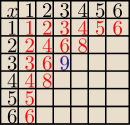
Hajtowy: Czerwone liczby to jest |A| a więc jest ich 16

	16
Tak więc		wg mnie
	36

ZKS: Zad. 1 a) 320 b) 372. Chyba że ja coś nie tak liczę.

Piotr 10: Na ile sposobów możemy postawić 5 książek na półce obok siebie tak, aby książki ABC stały obok siebie w dowolnym porządku? Na trzy sposoby mogę przemieszać książki ABC − 3 sposoby Mogę z nich utworzyć ciąg(dowolny porządek) − 3! Resztę książek na 2! 3*3!*2!=3*6*2=6*6=36

Piotr 10: A mniejszy od 9, myślałem ze nie mniejszy od 9 Więc Ok Twoje rozwiązanie

Piotr 10: Ile jest liczb trzycyfrowych o różnych cyfrach: a) nieparzystych I cyfra parzysta 4 sposoby II cyfra parzysta 4 sposoby III cyfra nieparzysta 5 sposobów 4*4*5=80 v I cyfra nieparzysta 5 sposobów II cyfra parzysta 5 sposobów III cyfra nieparzysta 4 sposoby 5*5*4=100 v I cyfra parzysta 4 sposoby II cyfra nieparzysta 5 sposobów II cyfra nieparzysta 4 sposoby 4*5*4=80 v I cyfra nieparzysta 5 sposobów II cyfra nieparzysta 4 sposoby III cyfra nieparzysta 3 sposoby 5*4*3=60 80+100+80+60=320

ZKS: Trochę inaczej liczyłem. Ma być to liczba nieparzysta oraz cyfry nie mogą się powtarzać to na końcu musi stać liczba nieparzysta i mamy takich opcji 5 na pierwszym miejscu nie może stać cyfra 0 oraz ta co stoi na końcu więc mamy opcji 8 na drugim miejscu nie może stać cyfra co stoi na początku i końcu ale liczymy już 0 więc 8 z reguły mnożenia otrzymujemy 8 * 8 * 5 = 320.

Piotr 10: b) większych od 483 1*1*4=4 v 1*1*8=8 v 1*9*8=72 5*72=360 360+4+8=372

Piotr 10: Ja to zawsze wolę na chłopski rozum wypisywać, na sprawdzianie też tak leciałem, że wszystko wypisywałem sobie ZKS możesz wejść https://matematykaszkolna.pl/forum/227707.html ?

Piotr 10: Ze zbioru {4,5,6,8,9} losujemy dwie liczby ze zwracaniem tworząc liczbę dwucyfrową. Jakie jest prawdopodobieństwo, że wylosowana liczba: a) będzie parzysta IΩI=5²=25 ( bo w. z powtórzeniami) IAI=5*3=15

	15		3
P(A)=		=
	25		5

b)podzielna przez 3 Suma cyfr musi być podzielna przez 3 IΩI=25 IBI={4;5} ; {4;8} ; (5;4) ; (5;9} ; (6;6} ; ( 6;9} ; (8;4} ; (9;6} {9;9}

	9
P(B)=
	25

Piotr 10: Pomyłka bez (5;9} powinno być więc masz ok