Planimetria
Radek:
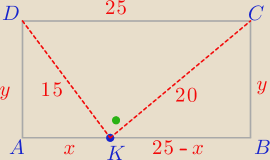
Punkt K należący do boku AB prostokąta ABCD połączono odcinkami z wierzchołkami C i D Oblicz
długości boków tego prostokąta wiedząc, że |DK|=15, |KC|=20 a kąt DKC jest prosty
|DC|
2=15
2+20
2
|DC|
2=625
|DC|=25
25y=300
y=12
BC=12
Mogę tutaj korzystać z podobieństwa trójkątów ?
12 gru 23:37
ICSP: i egzaminator ma się domyślić skąd ta proporcja ?
12 gru 23:40
Radek:
O Ci teraz chodzi ?
12 gru 23:44
Radek: ΔDKC∼ΔKCB ?
12 gru 23:45
ICSP: Jeżeli liczysz coś w planimetrii trzeba napisać dlaczego trójkąty są podobne oraz dla których
trójkątów układasz proporcje
Tójkąty ... są podobne ponieważ mają te same katy ... oraz ...
Z podobieństwa trójkąta .... i trójkąta ... dostaje proporcje
Nikt nie będzie się domyślał o co ci może chodzić

12 gru 23:46
Radek:
OK. A czy zapis 23:45 wystarczy ?
12 gru 23:47
ICSP: Jeszcze dodaj jedna linijkę tekstu dlaczego są podobne. Wiem, że to oczywiste, ale należy to
napisać

12 gru 23:48
ICSP: Dalej ok
y = 12
12 gru 23:49
Radek: Czyli muszę zaznaczyć jeszcze kąty na tym rysunku, żeby napisać cechę podobieństwa ?
12 gru 23:52
ICSP: katy masz zaznaczone np ∡ADC
12 gru 23:53
Radek:
Czyli piszę tak, że trójkąty ΔDKC∼ΔKBC ponieważ ∡KBC=∡DKC, mają wspólny bok KC
ok ?
12 gru 23:57
ICSP: Osobiście nie znam cechy podobieństwa trójkątów opartej na 1 kącie i jednym boku

12 gru 23:59
13 gru 00:01
Radek: ∡KCB=∡KDC dopisałem

13 gru 00:03
ICSP: teraz dobrze

13 gru 00:04
Radek:
Dzięki i dobranoc

13 gru 00:04
 Punkt K należący do boku AB prostokąta ABCD połączono odcinkami z wierzchołkami C i D Oblicz
długości boków tego prostokąta wiedząc, że |DK|=15, |KC|=20 a kąt DKC jest prosty
|DC|2=152+202
|DC|2=625
|DC|=25
Punkt K należący do boku AB prostokąta ABCD połączono odcinkami z wierzchołkami C i D Oblicz
długości boków tego prostokąta wiedząc, że |DK|=15, |KC|=20 a kąt DKC jest prosty
|DC|2=152+202
|DC|2=625
|DC|=25





