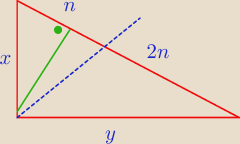
Planimetria Radek: W trójkącie prostokątnym dwusieczna kąta prostego dzieli przeciwprostokątną na odcinki, których stosunek długości wynosi 1:2. W jakim stosunku wysokość poprowadzona z wierzchołka kąta prostego dzieli przeciwprostokątną ?

x		y
	=
n		2n

2nx=yn /2n

	y
x=		ale co dalej ?
	2

Mila:

y
	=2
x

Teraz skorzystaj z podobieństwa Δ na jakie został podzielony trójkąt o przyprostokątnych x i y=2x.

matyk: Dalej geometra?

Radek: Jak tutaj zapisać tę proporcję ? Tak dalej geometria, aż do skutku

Mila:

	2x		h
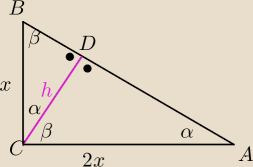
ΔCDB∼ΔABC⇔		=		stąd h=....
	x		BD

(bok 2x leży naprzeciw kąta β, bok x leży naprzeciw kąta α w ΔABC, bok h leży naprzeciw kąta β, bok BD leży naprzeciw kąta α w ΔCDB) Napisz dalej proporcję z ΔABC i ΔADC

Radek: hx=2x|BD|

	2
h=
	|BD|

CB		AB
	=
h		2x

Radek: Czemu Pani korzysta akurat z podobieństwa trójkątów ?

Mila: Korzystam z podobieństwa, bo to najkrótszy sposób i najłatwiej obliczyć AD i BD Napisałam wcześniej:

2x		h		1
	=		⇔h=2*|BD| stąd BD=		h
x		BD		2

Druga proporcja:

2x		AD
	=		⇔|AD|=2h
x		h

Szukany stosunek

AD		2h		4
	=		=		=4:1
BD		1   h 2		1

Radek: Dziękuję bardzo za dokładne wytłumaczenie, a mogę jeszcze prosić o pomoc w tym zadaniu: https://matematykaszkolna.pl/forum/226534.html ?