planimetria
Radek:
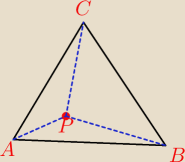
Wykaż, że jeśli punkt P jest punktem wewnętrznym trójkąta ABC, to prawdziwa jest nierówność
|AP|+|BP|<|AC|+|BC|
|AC|<|AP|+|CP|
|BC|<|BP|+|CP|
|AC|+|BC|<|AP|+|BP|+2|CP|
Znowu nie wiem co jest źle ?
Proszę niech ktoś wytłumaczy dokładnie
7 gru 19:53
Radek: Nie proszę o gotowe rozwiązanie tylko wskazówkę co robię źle..
7 gru 20:02
Bizon:
... przecież dowiodłeś −

7 gru 20:08
Radek: ale to 2|CP| mi tam nie pasuje

7 gru 20:10
Radek: ?
7 gru 20:19
Radek: up ?
7 gru 20:26
Radek: ?
7 gru 20:38
Lorak: dlaczego 2|CP| Ci nie pasuje?
7 gru 20:39
MQ: A możesz używać tw. sinusów i tw. cosinusów?
7 gru 20:40
Radek:
Nie.
7 gru 20:42
Radek:
|AP|+|BP|<|AC|+|BC bo tutaj nie mam 2|CP|
7 gru 20:45
Radek: ?
7 gru 20:50
7 gru 20:56
Radek:
Rozwiązanie gotowe czyli brak rozwiązania

7 gru 21:04
Lorak: Na podstawie tego rozwiązania możesz stwierdzić co robiłeś źle...
A to chyba na jedno wychodzi, gdyby ktoś powiedział Ci co robisz źle.
Ale jeśli nie lubisz linków, to ok

7 gru 21:07
Radek: Wolę, żeby ktoś podpowiedział niż podawał gotowy wynik z którego i tak nic nie zrozumiem. Uczę
się na błędach a nie na gotowcach
7 gru 21:08
Radek: Pomoże ktoś bo nadal nie rozumiem ?
9 gru 17:16
Mila:
Wszystko masz dobrze zapisane , lecz to nie prowadzi do celu.
9 gru 18:02
Radek:
Ja muszę wszystkie przypadki rozważyć ?
AC<AP+CP
AB<AP+BP
CB<CP+BP
i z tego mam:
AC+AB+CB<2|AP|+2|CP|+2|BP| /2
| AC+CB+AB | |
| <AP|+|CP|+|BP| |
| 2 | |
Ale ja udowodniłem, ze suma długości wierzchołków od punkt P jest większa od połowy obwodu. Co
jest nie tak ?
9 gru 18:14
Mila:
No i to jest prawda.
Suma odległości wierzchołków Δ od punkt P jest większa od połowy obwodu Δ.
To jest też prawda dla czworokąta. Masz gotowy dowód.
Ale Tobie polecono co innego wykazać.
Dlaczego nie skorzystasz z podpowiedzi Lorak.
Jeśli chcesz aby kontynuować Twój pomysł, to poczekaj cierpliwie. Mam inny pomysł na dowód.
9 gru 18:26
Radek:
Wie ktoś jak dokończyć to zadania, ale moim sposobem ?
21 gru 20:04
Radek: Pomoże ktoś ? Bardzo zależy mi na tym dowodzie

22 gru 17:15
Radek: ?
22 gru 17:41
Radek: 
22 gru 18:09
Radek: ?
25 gru 19:36
Radek: Nikt ?
25 gru 19:47
Radek: ?
25 gru 21:53
Radek:

26 gru 20:27
Godzio:
Chodzi o to zadanie z tematu ? Bo nie chce mi się czytać

?
26 gru 20:29
Radek: Tak i o post 18:26 bo bez spmu raczej bym się nie doczekał

26 gru 20:32
Godzio:
I o co dokładnie chodzi ? Pokusiłem się o przeczytanie, chcesz wskazówkę czy dowód ? (bo z tego
co czytam to tego drugiego chyba nie)
26 gru 20:39
Radek:
Dokończyć ten dowód ale w ten sposób który ja zacząłem

26 gru 20:41
Godzio:
No dobra, tylko że nie zawsze się tak da, generalnie powiem jak ja to robię przy takich
zadaniach.
Po pierwsze rysunek i podstawowe nierówności − właśnie te, z których skorzystałeś, ale jak
widać nie dały żadnego efektu, czyli nie tędy droga, jeżeli standardowe nierówności nic nie
dają trzeba stworzyć "nowe" nierówności, a jak je otrzymać ? Ano coś sobie dorysować, spróbuj
przedłużyć odcinek AP albo BP do jednego z boków trójkąta i znów kombinuj z nierównościami,
26 gru 20:47
Radek:
OK. dziękuję zaraz spróbuje
26 gru 20:48
Godzio:
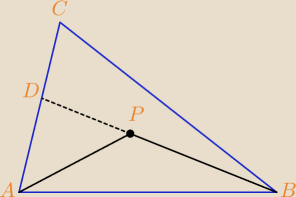
Teza: |AP| + |BP| < |AC| + |BC|
Przez przedłużenie odcinka BP otrzymaliśmy dwa nowe trójkąty, z których mamy kolejne
nierówności, może akurat coś się uda

|AD| + |DP| > |AP|
|CD| + |BC| > |BD| dodajemy
|AD| + |CD| + |DP| + |BC| > |AP| + |BD| = |AP| + |DP| + |PB| / − |DP|
|AC| + |BC| > |AP| + |PB|
Jak widać teza jest natychmiastowa. Co do nierówności to był kompletny strzał, poprzednie
nierówności nic nie dały, to skorzystałem z zupełnie nowych, następnym krokiem gdyby to nie
podziałało, pewnie byłoby mieszanie tamtych z tymi.
26 gru 20:52
Radek:
Dzięki. Tylko ja na to wpaść nie mogłem

26 gru 20:53
Godzio:
Dlatego masz robić zadania, ile kombinujesz nad zadaniem zanim zrezygnujesz ? Ja pamiętam
siedziałem po kilka godzin, nawet nad jednym zadaniem, aż rozwiązałem !

26 gru 21:01
Eta:

26 gru 21:02
Radek:
Godzio czas ucieka, a mam jeszcze analityczną do opanowania.
26 gru 21:04
Ajtek:
Radek spokojna uczesana, czasu jeszcze sporo

.
26 gru 21:05
Piotr 10: Geometria analityczna piękna jest

26 gru 21:05
Godzio:
Łohoho, a niektóre zadania od
Ety ile czasu robiłem

26 gru 21:06
Ajtek:
Godzio, bo Eta miała Ciebie na oku. Dawała Tobie takie zadanka wersja lajcik

26 gru 21:07
 Wykaż, że jeśli punkt P jest punktem wewnętrznym trójkąta ABC, to prawdziwa jest nierówność
|AP|+|BP|<|AC|+|BC|
|AC|<|AP|+|CP|
|BC|<|BP|+|CP|
|AC|+|BC|<|AP|+|BP|+2|CP|
Znowu nie wiem co jest źle ?
Proszę niech ktoś wytłumaczy dokładnie
Wykaż, że jeśli punkt P jest punktem wewnętrznym trójkąta ABC, to prawdziwa jest nierówność
|AP|+|BP|<|AC|+|BC|
|AC|<|AP|+|CP|
|BC|<|BP|+|CP|
|AC|+|BC|<|AP|+|BP|+2|CP|
Znowu nie wiem co jest źle ?
Proszę niech ktoś wytłumaczy dokładnie







 ?
?


 Teza: |AP| + |BP| < |AC| + |BC|
Przez przedłużenie odcinka BP otrzymaliśmy dwa nowe trójkąty, z których mamy kolejne
nierówności, może akurat coś się uda
Teza: |AP| + |BP| < |AC| + |BC|
Przez przedłużenie odcinka BP otrzymaliśmy dwa nowe trójkąty, z których mamy kolejne
nierówności, może akurat coś się uda  |AD| + |DP| > |AP|
|CD| + |BC| > |BD| dodajemy
|AD| + |CD| + |DP| + |BC| > |AP| + |BD| = |AP| + |DP| + |PB| / − |DP|
|AC| + |BC| > |AP| + |PB|
Jak widać teza jest natychmiastowa. Co do nierówności to był kompletny strzał, poprzednie
nierówności nic nie dały, to skorzystałem z zupełnie nowych, następnym krokiem gdyby to nie
podziałało, pewnie byłoby mieszanie tamtych z tymi.
|AD| + |DP| > |AP|
|CD| + |BC| > |BD| dodajemy
|AD| + |CD| + |DP| + |BC| > |AP| + |BD| = |AP| + |DP| + |PB| / − |DP|
|AC| + |BC| > |AP| + |PB|
Jak widać teza jest natychmiastowa. Co do nierówności to był kompletny strzał, poprzednie
nierówności nic nie dały, to skorzystałem z zupełnie nowych, następnym krokiem gdyby to nie
podziałało, pewnie byłoby mieszanie tamtych z tymi.



 .
.


