Udowodnij nieróność.
Ambryll: Wykaż, że jeśli punkt P jest punktem wewnętrznym trójkąta ABC to prawdziwa jest nierówność:
|AP|+|BP|<|AC|+|BC|. Proszę o pomoc.

3 maj 16:58
f:
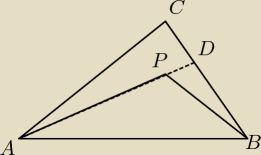
|AC| + |CB| = |AC| + |CD| + |DB| > |AD| + |DB| = |AP| + |PD| + |DB| > |AP| + |PB|
3 maj 17:13
Ambryll: |AC| + |CB| = |AC| + |CD| + |DB| > |AD| + |DB| = |AP| + |PD| + |DB| > |AP| + |PB|
A mogę prosić o wytłumaczenie tego zapisu? Tak po kolei


3 maj 17:21
f: ok

|CB| = |CD| + |DB| (D leży na CB)
nierówność trójkąta:
|AC|+|CD| > |AD|
potem:
|AD| = |AP|+|PD| (P leży na AD)
i znów nierówność trójkąta:
|PD|+|DB| > |PB|
3 maj 17:43
Ambryll: Czyli po rozpisaniu, itd.:
|AC|+|CB|+|BD|>|AD|
|AD|+|PA|+|DB|>|PB|
|AC|+|CB|+|BD|+|AD|+|PA|+|DB|>|AD|+|PB|
|AC|+|CB|+|PA|>|PB|
|AC|+|CB|>|PB|+|AP|
Dobrze?

3 maj 18:11
Ambryll: CND.
3 maj 18:11
f: nie, po kolei:
|AC| + |CB| = |AC| + |CD| + |DB|
bo |CB| = |CD| + |DB| (D leży na CB)
z nierówności trójkąta:
|AC|+|CD| > |AD|
mamy:
|AC| + |CB| = |AC| + (|CD| + |DB|) > |AD| + |DB|
czyli:
|AC| + |CB| > |AD| + |DB|
teraz, ponieważ:
|AD| = |AP|+|PD| (P leży na AD)
|AC| + |CB| > |AD| + |DB| = |AP|+|PD| + |DB|
czyli:
|AC| + |CB| > |AP|+|PD| + |DB|
ponieważ:
|PD|+|DB| > |PB|
to:
|AP|+ |PD|+|DB| > |AP| + |PB|
a jako, że:
|AC| + |CB| > |AP|+|PD| + |DB|
to:
|AC| + |CB| > |AP| + |PB|
3 maj 18:59

 |AC| + |CB| = |AC| + |CD| + |DB| > |AD| + |DB| = |AP| + |PD| + |DB| > |AP| + |PB|
|AC| + |CB| = |AC| + |CD| + |DB| > |AD| + |DB| = |AP| + |PD| + |DB| > |AP| + |PB|


 |CB| = |CD| + |DB| (D leży na CB)
nierówność trójkąta:
|AC|+|CD| > |AD|
potem:
|AD| = |AP|+|PD| (P leży na AD)
i znów nierówność trójkąta:
|PD|+|DB| > |PB|
|CB| = |CD| + |DB| (D leży na CB)
nierówność trójkąta:
|AC|+|CD| > |AD|
potem:
|AD| = |AP|+|PD| (P leży na AD)
i znów nierówność trójkąta:
|PD|+|DB| > |PB|
