tryg
Radek:
Określ zbiór wartości D=<−π,π> f(x)=cosx−1
ZW=<−2,2>
5 gru 20:35
Radek:
Jak zamienić 3 radiany na stopnie ?
5 gru 20:38
krystek: <−1,1> i obniż o 1
5 gru 20:38
Radek:
Dobry wieczór
5 gru 20:39
krystek:
3 rad⇒ x stopni
π rad⇒180 stopni
−−−−−−−−−−−−−−−−−−−−−−−
5 gru 20:40
5 gru 20:41
Radek: ?
5 gru 20:46
Saizou : | | 540 | |
x= |
| bo ma być w radnianach  |
| | π | |
5 gru 20:47
bezendu:
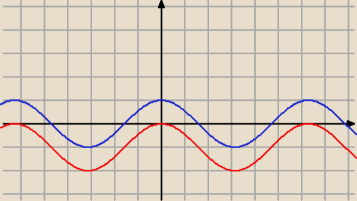
to jest wykres do cosx−1 !
5 gru 20:48
Radek: radiany na stopnie ?
5 gru 20:49
Eta:
1rd≈57
o to 3rd≈172
o
| | 180o | | 540o | | 540o | |
3rd* |
| = |
| = |
| ≈ 172o |
| | πrd | | π | | 3,14 | |
5 gru 20:50
krystek: ale musisz miec np 3π
5 gru 20:51
5 gru 21:05
Radek:
Już do główki puk puk i wiem
5 gru 21:06
Radek:
| | π | |
a jak narysować sin(x− |
| ) |
| | 4 | |
to będzie sinx przesunięty o 45
0 ?
5 gru 21:09
5 gru 21:12
Radek:
ale takiego czegoś tam niema sin|x| ?
5 gru 21:14
Eta:
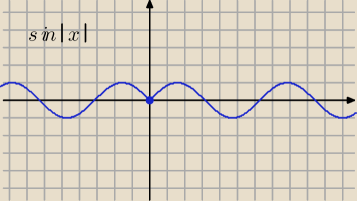
5 gru 21:17
krystek: zauważ ,że sinI−xI=sinIxI sym wzgledem osi OY
5 gru 21:17
Radek:
Może Pani wytłumaczyć mi to przekształcenie ?
5 gru 21:17
krystek: Kreslisz sinx dla x dodatnich a dla ujemnych odbijasz sym względem osi OY
5 gru 21:20
Radek:
A takie coś 3*|cosx| ?
5 gru 21:20
krystek: cosx
nastepnie IcosxI ( ujemne nad os OX)
3*IcosxI zwiększasz 3 krotnie wartosci
5 gru 21:22
Eta:
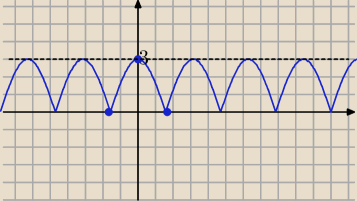
5 gru 21:26
Radek:
już ostatnie wykres
√1+tg2x
Dobrze przekształciłem ?
5 gru 21:26
Radek: ?
5 gru 21:40
pigor: | | 1 | | 1 | |
...√1/cos2x= |
| = |
| i cosx≠0 |
| | √cos2x | | |cosx| | |
5 gru 21:46
Radek:
pigor a czemu nie może być cosx w mianowniku ?
5 gru 21:46
Radek: ?
5 gru 21:52
Radek:
| | x | |
Jeszcze ostatnie tg |
| ? |
| | 2 | |
5 gru 22:06
Radek: ?
5 gru 22:21
Saizou : taki rozciągnięty tangens
5 gru 22:28
Radek:
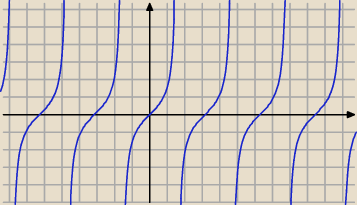
jak to rozciągnąć ?
5 gru 22:29
Saizou : ja zazwyczaj robię tak
| | π | |
jak się rozciąga to zmienia się asymptota z |
| na π |
| | 2 | |
| | π | | | |
wartość 1 jest dla |
| , bo y=tan( |
| )=1 |
| | 2 | | 2 | |
i tak dalej....
5 gru 22:35
Radek:
Dziękuję a jeszcze zobacz na moje pytanie 21:46 ?
5 gru 22:36
Saizou : a skąd wiesz czy masz dodatni cosinus
no i wzorek jest
√a2=lal
5 gru 22:37
Radek: wiem że jest wzorek
5 gru 22:38