Logika Zbiory
Pomocy: Hej mam pytanie o zbiory i przykład który zabardzo nie kminie.
Oblicz AuB AnB A\B B\A
A=(2,3) u {4} B= [2,4)
ogolnie wiem o co chodzi ale mam problem z wyznaczeniem tego
Napisze jak ja to zrobilem
AuB = (2,3,4)
AnB = [2,4) (tego nie jestem pewien )
A\B = tego nie wiem jak zapisac
B\A = tego tez
29 lis 14:18
29 lis 14:25
Pomocy: No ok wiem co trzeba zrobić ale nie wiem jak to zapisać na tym przykładzie. Przeciez te same
liczby sa w A i B
29 lis 14:31
Krzysiek: A∪B=[2,4]
do zbioru A należy 4, która nie należy do zbioru B i odwrotnie z '2'
czyli 2 i 4 należą do sumy.
A∩B czyli część wspólna,
A∩B=(2,3)
Najlepiej narysuj to sobie i sprawdzaj po kolei
29 lis 14:36
Bogdan:
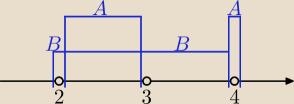
A∪B = <2, 4>
A∩B = (2, 3)
A \ B = {4}
B \ A = {2}∪<3, 4)
29 lis 14:43
Pomocy: Troche lipne to zadanie xD Robilem juz sporo przykladow ale tego nie moge zakminic juz dawno
narysowalem sobie i dalej nie mam pojecia jak to zapisac xD ale i tak thx za odpowiedz
29 lis 14:45
gebra:
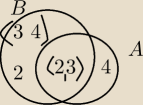
1. gdy wymieniasz elementy zbioru zapis w {} gdy przedziały zapis w () lub [] jeśli skrajne
należą.
2. A∪B = [2,4] dlaczego ? bo zb A zawiera prawie całkowicie [poza 4] B więc suma
to od lewej zaczyna się od 2, rośnie do 3, w zb B zachowuje przejscie od 3−4 a A dodaje $ do
zbiorów więc mam jak wyżej.
3. a∩B (2,3) więc ich przekrój 2 nie należy, bo tylko [2 w B oeraz 3 nie należy bo w a 3)
4. A\B zbiór A, minus czesc przekroju z B więc {4}
B\A = {2} u (3,4)
29 lis 14:45
gebra: na samym dole [3,4) , mały błąd się wkradł , 3 należy bo mieści się w przedziale B od 2−−−4
29 lis 14:47
gebra: mogę to jeszcze inaczej wyjaśnić jeśli chcesz, zwłaszcza odejmowanie
A\B=A∩B'
ANALOGICZNIE
B\A=B∩A'
29 lis 14:50
Pomocy: ok thx za pomoc teraz juz nawet rozumiem troche musze teraz to przecwiczyc troche xD
29 lis 15:00
 A∪B = <2, 4>
A∩B = (2, 3)
A \ B = {4}
B \ A = {2}∪<3, 4)
A∪B = <2, 4>
A∩B = (2, 3)
A \ B = {4}
B \ A = {2}∪<3, 4)
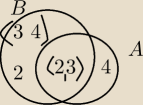 1. gdy wymieniasz elementy zbioru zapis w {} gdy przedziały zapis w () lub [] jeśli skrajne
należą.
2. A∪B = [2,4] dlaczego ? bo zb A zawiera prawie całkowicie [poza 4] B więc suma
to od lewej zaczyna się od 2, rośnie do 3, w zb B zachowuje przejscie od 3−4 a A dodaje $ do
zbiorów więc mam jak wyżej.
3. a∩B (2,3) więc ich przekrój 2 nie należy, bo tylko [2 w B oeraz 3 nie należy bo w a 3)
4. A\B zbiór A, minus czesc przekroju z B więc {4}
B\A = {2} u (3,4)
1. gdy wymieniasz elementy zbioru zapis w {} gdy przedziały zapis w () lub [] jeśli skrajne
należą.
2. A∪B = [2,4] dlaczego ? bo zb A zawiera prawie całkowicie [poza 4] B więc suma
to od lewej zaczyna się od 2, rośnie do 3, w zb B zachowuje przejscie od 3−4 a A dodaje $ do
zbiorów więc mam jak wyżej.
3. a∩B (2,3) więc ich przekrój 2 nie należy, bo tylko [2 w B oeraz 3 nie należy bo w a 3)
4. A\B zbiór A, minus czesc przekroju z B więc {4}
B\A = {2} u (3,4)