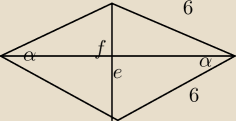
Kosinus kąta ostrego rombu którego bok ma długość 6 jest równy U{2}{3}. Oblicz p kamczatka:

	2
Kosinus kąta ostrego rombu którego bok ma długość 6 jest równy		. Oblicz pole tego rombu.
	3

przekątne to e i f.

	e
cosα=
	6

2		e
	=
3		6

e=4 dobrze robię ?

matyk: Niestety ale źle. α to cały kąt, a ty go traktujesz jak połowę

kamczatka:

	e
α to cały kąt czyli cosα=
	6

kamczatka: ?

kamczatka: to jak to obliczyć

kamczatka: nikt nie wie ?

5-latek: Aby policzyc to zadanie nie potrzeba liczyc przekatnych Wzor na pole rombu jest taki P=a²*sinx gdzie x −−to kat

	2
Masz podany cos x=
	3

	4		5		5		√5
Wiec sinx2+cos2x=1 to sin2x=1−cos2x =1−		=		to sinx=√		=
	9		9		9		3

	√5
P=62*		= policz
	3

~r.: cos^α₂ = ^f₂ : 6 i dalej już samemu...

kamczatka: ten wzór co podał 5−latek to chyba ze wzorów na maturę rozszerzoną?

matyk: Nie, to wzór z podstawy na pole trójkąta. Równoległobok, to 2 trójkąty przystające

5-latek: https://matematykaszkolna.pl/strona/866.html Popatrz tu na wzory Ja nie rozrozniam czy to podstawa czy rozszerzenie gdyz ja to mialem dawno

kamczatka: ok dzięki.