Funkcje cyklometryczne i odwrotne - wykres V.Abel: Witam, mam ogromną prośbę o wytłumaczenie jak rysuje się i jak rozwiązuje się, aby dojść do wyniku, który można zobrazować takie funkcje: a) f(x)=arccos(cosx) b) g(x)=cos(arccosx) Bardzo proszę o wyjaśnienia i pomoc w zrozumieniu rysowania tego typu wykresów funkcji

PW: Popatrz tutaj 223292

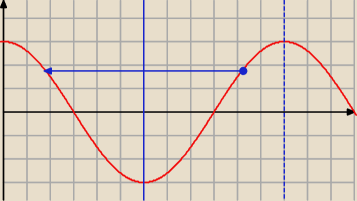
Trivial: Definicja funkcji arccos jest następująca: arccos(y) = x ⇔ y = cos(x) ∧ x ∊ [0,π] arccos : [−1,1] → [0,π] cos : R → [−1,1] a) arccos ∘ cos : R → arccos([−1,1]) ≡ R → [0,π] arccos(cos(x)) = u ⇔ cos(x) = cos(u) ∧ u ∊ [0,π] Innymi słowy, musimy wybrać taką wartość z przedziału u ∊ [0,π], aby cos(x) = cos(u). Liczba u jest wartością funkcji f w punkcie x. Najpierw definiujemy funkcję s₁(x), która sprowadzi x do przedziału [0,2π)

	x
s1(x) = x − [		]*2π
	2π

Mając x w przedziale [0,2π) definiujmy funkcję s₂, która sprowadzi x do przedziału [0,π].

	⎧	x, gdy x∊[0,π]
s2(x) =	⎨		(rysunek)
	⎩	2π−x, gdy x∊(π,2π)

Zapiszmy s₂ zwięźlej: s₂(x) = π − |x−π| A zatem, funkcja f(x), która sprowadzi x od razu do przedziału [0,π] ma postać:

	x
f(x) = s2(s1(x)) = π − |x − [		]*2π − π|.
	2π

b) cos ∘ arccos : [−1,1] → cos([0,π]) ≡ [−1,1] → [−1,1] cos(arccos(x)) = x

V.Abel: Trivial − jesteś wielki Dzięki stary Pw również ps muszę to przeanalizować, jakby co odezwę się jeszcze