. Piotr 10: Niech A i B będą dowolnymi zdarzeniami. Wykaż, że: P(A)+P(A' ∩ B) = P(B)+P(A∩ B') Proszę o pomoc

Piotr 10: ?

Piotr 10: P(A'∪B)=P(A')+P(B) − P(A'∩B) P(A∪B')=P(A)+P(B') − P(A∩B') P(A)+P(A')+P(B) − P(A'∪B)=P(B)+P(A)+P(B') − P(A∪B') Nie wiem, nie rozumiem tego w ogole

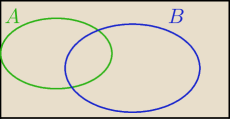
Mila: P(A)+P{A'∩B)=P(A)+P(B\A)=P(A)+P(B)−P(A∩B) Podobnie z drugą stroną

Mila: Narysować dokładniej?

Piotr 10: Chwilka

Piotr 10: P(A' ∩ B)=P(B−A) z tego wynika chyba P(A ∩ B')=P(A−B) ?

Piotr 10: P(A)+P(B−A)=P(B)+P(A−B) i co dalej ?

Mila: A\B ma być . Poprawię później. Teraz mam gości.

Piotr 10: P(A)+P(B) − P(A∩B)= P(B)+P(A) − P(A∩B) L_s=P_s Wyszło w końcu coś mi dzisiaj

Piotr 10: P(A−B)=P(A) − P(A∩B) wszystko spoko tylko

	1
P(A)≤
	5

	1
P(A∩B) ≥
	8

I jak to teraz zrobić? Bo mam nierówności i nie wiem jak to sie robi

Piotr 10: Dane sa dwa zdarzenia A,B ⊂Ω takie ze P(A')≥ 2/3 i P(A∩ B) ≥1/8. Wykaz, ze P(A∪B) ≤ 7/12 P{A U B)=P(A)+P(B) − P(A∩B)

2
	≤ 1 − P(A)
3

P(A) ≤ 1/3 Jak znaleźć P(B) ?

Piotr 10: A niech mnie szlak trafi, dziękuję za pomoc..

Mila: Bez nerwów, już jestem, najpierw treść 17:27 Jak?

Piotr 10: To dobrze, że jesteś. Chodzi mi o odejmowanie głownie. Dane są dwa zdarzenia A, B⊂ Ω takie, że

	1		1		1
P(A)= ≤		i P(A ∩ B) ≥		. Czy może być P(A−B)=
	5		8		10

Nie umiem tych nierówności odjąć

Piotr 10: Udowodnij, że P(A)+P(A' U B)=P(B)+P(A U B' ) P(A' U B)=P(A')+P(A ∩ B) P(A U B')=P(B') + P( A ∩ B) P(A)+P(A')+P(A ∩ B)=P(B)+P(B') + P( A ∩ B) P(A)+1−P(A)+P(A ∩ B)=P(B)+1−P(B} + P( A ∩ B) L_s=P_s ?

Mila:

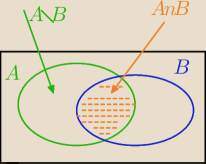
1		1		1		3
	=P(A\B)=P(A)−P(A∩B)≤		−		=
10		5		8		40

(zwiększyłam odjemną, zmniejszyłam odjemnik)

1		4		3
	=		>		sprzeczność
10		40		40

Piotr 10: Ale dlaczego ≤ ? tego nie rozumiem

Mila: 18:46 dobrze. 17:58 nic nie pominąłeś w treści.

Piotr 10: Nic właśnie, to zadanie ze zbioru Pazdro numer 7.115

Mila: np. 10−3<12−1

Piotr 10: nie rozumiem

Mila: To popatrz na rysunek 18:49

	1		1
Gdyby P(A\B)=		i P(A∩B)=		(najmniejszą wartość podstawiam), to mamy:
	10		8

	1		1		4+5		9		1		1
P(A)=		+		=		=		>		a masz warunek, że P(A)≤
	10		8		40		40		5		5

Piotr 10: Dlaczego ''ponieważ A∩(A∩B)=∅'' ) https://matematykaszkolna.pl/forum/125301.html ?

Piotr 10: ok wiem już