prawdopodobieństwo m: Wiadomo, że P(A')=0,9, P(A∪B)=0,28, P(A'∪B')=0,98. Oblicz P(B'), P(A'∩B'), P(A−(A∩B)). Próbowałem wzorami z tablic i wzorami, które podała nam nauczycielka, ale nic sensownego nie wychodzi. Od znajomego dostałem wzór P(A'∩B')=P(A∪B)', ale jak mam go wykorzystać?

Aga1: P(A∪B)'=1−P(A∪B) Podobnie A^'∪B^'=(A∩B)^'

m: Dzięki Aga.

pigor: ... no to może np. tak : otóż, P(A')=0,9 ⇒ P(A)=1−0,9=0,1 ; 2) z prawa Morgana dla zbiorów : P(A'∩B')=P(AUB)'=1−P(AUB)=1−0,28=0,72 , z prawa Morgana : P(A'UB')=0,98 =P(A∩B)' ⇒ P(A∩B)=1−0,98=0,02 3) ponieważ A∩(A∩B)=∅ ⇒ P(A −(A∩B))=P(A)−P(A∩B)=0,10 − 0,02= 0,08 , P(AUB)=0,28 ⇒ P(A)+P(B)−P(A∩B)=0,28 ⇒ P(B)=0,28−P(A)+P(A∩B) ⇒ P(B)=0,28−0,10+0,02 =0,2 ⇒ 1) P(B)=1−0,2 = 0,8 i tyle . ...

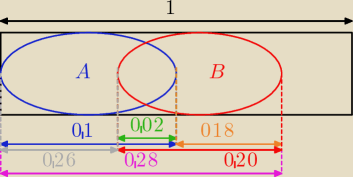
Gustlik: Wiadomo, że P(A')=0,9, P(A∪B)=0,28, P(A'∪B')=0,98. Oblicz P(B'), P(A'∩B'), P(A−(A∩B)). P(A')=0,9 ⇒ P(A)=0,1 P(A'∪B')=P(A∩B)'=0,98 (prawa de Morgana) ⇒ P(A∩B)=0,02 P(A'∩B')=P(AUB)'=1−P(AUB)=1−0,28=0,72 (prawa de Morgana) Z rysunku widać, że P(B\A)=0,28−0,1=0,18 P(B)=P(B\A)+P(A∩B)=0,18+0,02=0,20=0,2 P(B')=1−P(B)=1−0,2=0,8 P(A\(A∩B))=0,28−0,02=0,26 Więcej na temat praw de Morgana tutaj: https://matematykaszkolna.pl/strona/1060.html . Warto je znać, bo bez nich rozwiązanie takiego zadania to kombinacja alpejska.

Gustlik: Wkradł sie błąd: ma być: P(A\(A∩B))=0,1−0,02=0,08 (szary kolor), poza tym dobrze.